Luogu 4723 求解线性递推
给定$k$阶线性递推${F}$的前$k$项,$F_0,F_1,\cdots ,F_{k-1}$,以及系数$a_1,a_2,\cdots ,a_k$满足:
$$
F_n =\sum_{i=1}^k F_{n-i} \cdot a_i (n\ge k)
$$
求$F_n$,其中$n\leq 10^{18},k\leq 6\times 10^4$。
因为$n$非常大,所以之前的特征根法在这里没有什么用,因为需要解一个$10^5$阶的方程,肯定是解不出来的,所以没法求出它的通项。
首先第一想法是矩阵快速幂
设初始向量是$\overrightarrow a$然后给它乘上$M^{n-k}$
直接算复杂度就是$O(k^3 \log n)$
这个东西肯定不是非常够接受。
然后介绍一个定理:
Cayley-Hamilton 定理
线性代数中一个非常重要的定理。这里就不证了。
首先讲一下基础概念:特征多项式。
举个例子,对于一个矩阵$M$而言,它的特征多项式是$\operatorname{char(M)}$(注意这是整体是一个多项式)
可以把$\operatorname{char}$看作一个函数,设自变量为$\lambda$,就是从$\mathbb{R}^{M\times N}\to \mathbb{R} [\lambda]$(从$M\times N$阶矩阵,映射到一个关于$\lambda$的一个多项式)
那么$\operatorname{char(M)} (\lambda) $就被定义为$\det (\lambda I-M)$(若矩阵大小为$K$,则这是一个$K$阶多项式。)
然后把它写成多项式的形式(特征多项式最高次项为$1$):
$$
\operatorname{char(M)}(\lambda)=\lambda ^k -\sum\limits_{i=1}^k a_i \lambda ^{k-i}
$$
然后Cayley-Hamilton 定理就是说
$$
\operatorname{char(M)}(M)=0
$$
即
$$
M^k=\sum_{i=1}^k a_i M^{k-i}
$$
然后两边同乘$M^{n-k}$,得到:
$$
M^{n-k}\cdot M^k=\sum_{i=1}^k a_i M^{n-k} M^{k-i}
$$
$$
M^n=\sum_{i=1}^k a_i \cdot M^{n-i}
$$
所以假如知道$a_i$,考虑怎么求矩阵快速幂:
大概就是把$M^n$拆成$n-1,n-2,\cdots ,n-k$的组合。
然后$n-1$可以拆成$n-2,\cdots ,n-k-1$这样一直变,最后一叠,就变成:
$$
M^n =\sum_{i=0}^{k-1} b_i M^i
$$
因此,假如要求$M^a\cdot M^b$,就是
$$
\big(\sum\limits_{i=0}^{k-1} b_i\cdot M_i \big)\big(\sum\limits_{i=0}^{k-1} c_i\cdot M_i \big)
$$
然后对$b$和$c$进行卷积:
$$
\sum_{i=0}^{2k-1} \sum_{j=0}^{i} b_j \cdot c_{i-j} M^i
$$
多了一些项,就用类似等于$a$的方式给它搞回去。
这个东西可以在$O(k^2\log n)$的时间复杂度之内求出。
当然需要知道$a$。
然后考虑$M$长什么样子(图中的$a$为题目给出的$a$)
$$
M=\begin{bmatrix} a_1 & a_2 & a_3 &\cdots &a_k \1 & 0 &0 &\cdots &0\ 0 & 1 &0 &\cdots &0\0 & 0 &1 &\cdots &0\ \vdots & \ddots & &\ & \vdots \\vdots & &\ddots & & \vdots\ \vdots & & &\ddots & \vdots\ 0 & 0 & \ldots & 1 & 0
\end{bmatrix}
\begin{bmatrix} f_n\ f_{n-1} \f_{n-2}\ \vdots \ f_{n-k+1}
\end{bmatrix}
\begin{bmatrix} f_{n+1}\ f_{n} \f_{n-1}\ \vdots \ f_{n-k+2}
\end{bmatrix}
$$
我猜会崩,所以先放张图:

对于这个东西考虑求出特征多项式(因为稀疏,所以考虑直接手算…)
然后这个题就做完了。
现在就相当于是给一个$2k-1$次多项式(就是上面那个$b$卷$c$的多项式),这里称为$d(M)$。然后要求一个$k$次多项式$r(M)$满足$r$和$d$是一样的。
因为$\operatorname{char(M)}(M)=\sum\limits_{i=0}^{k-1} a_i M^i=0$,然后把这个写成$b(M)$
$d(M)=b(M)\cdot g(M) +r(M)$
那么$r(M)\equiv d(M) \pmod {b(M)}$
然后现在由于你给任何多项式加或减这个$b(M)$,这个值都不变,所以考虑用这个给$d(M)$降次。
可以理解为:
假如现在由$x_0$满足$x_0^3=x_0^2+2x_0+3$。
那么像$x_0^{100}$就可以拆成$x_0^{99}+2x_0^{98}+3x_0^{97}$,而$x_0^{99}$又可以拆成$x_0^{98}+2x_0^{97}+3x_0^{96}$……然后这么一直拆下去
其实这就相当于对$x^3-x^2-2x-3$取模。
由于多项式除法是$O(k\log k)$的,所以总复杂度就是$O(k\log k\log n)$,就是每一次快速幂都这样做一次多项式取模。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
|
const int N=333333;
const int _G=3;
const int invG=332748118;
int k,n,m,K,AN;
int lim,totp;
inline int read_mod(){static int x;x=read();x%=mod;x+=x>>31&mod;return x;}
int tr[N],tf;
int inv[N];
int W[N],p[N],f[N],t[N];
int a[N],ans[N];
inline void tpre(int n)
{
if(tf==n)return;tf=n;R(i,0,n-1) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
}
void NTT(int *g,int rev,int n)
{
tpre(n);
static ull f[N<<1],w[N<<1];w[0]=1;
R(i,0,n-1) f[i]=(((ll)mod<<5)+g[tr[i]])%mod;
for(int l=1;l<n;l<<=1)
{
ull tG=fpow(rev?_G:invG,(mod-1)/(l+l));
R(i,1,l-1) w[i]=w[i-1]*tG%mod;
for(int k=0;k<n;k+=l+l)
{
R(p,0,l-1)
{
int tt=w[p]*f[k|l|p]%mod;
f[k|l|p]=f[k|p]+mod-tt;
f[k|p]+=tt;
}
}
if(l==(1<<10)) R(i,0,n-1) f[i]%=mod;
}
if(!rev)
{
ull invn=fpow(n);
R(i,0,n-1) g[i]=f[i]%mod*invn%mod;
}
else R(i,0,n-1) g[i]=f[i]%mod;
}
void px(int *f,int *g,int *p,int n){R(i,0,n-1)p[i]=1ll*f[i]*g[i]%mod;}
void poly_inv(int *f,int *g,int m)
{
int n=lim;
static int w[N<<1],r[N<<1],sav[N<<1];
w[0]=fpow(f[0]);
//printf("f0:%d w0:%d\n",f[0],w[0]);
for(int l=2;l<=n;l<<=1)
{
R(i,0,(l>>1)-1) r[i]=w[i];
cpy(sav,f,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);clr(r,l>>1);
cpy(sav,w,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);
R(i,l>>1,l-1) w[i]=(w[i]*2ll-r[i]+mod)%mod;
}
cpy(g,w,m+1);clr(sav,n);clr(w,n);clr(r,n);
}
void poly_times(int *f,int *g,int *p,int n,int m,int lim)
{
static int tmpf[N<<1],tmpg[N<<1];
for(m+=n,n=1;n<m;n<<=1);
clr(tmpf,n),cpy(tmpf,f,n);
clr(tmpg,n),cpy(tmpg,g,n);
NTT(tmpf,1,n),NTT(tmpg,1,n);
px(tmpf,tmpg,p,n),NTT(p,0,n);
clr(p+lim,n-lim);clr(tmpf,n),clr(tmpg,n);
}
void init(int n)
{
for(lim=1;lim<=n;lim<<=1,++totp);
tpre(lim);
int tG=fpow(3,mod>>totp);W[lim>>1]=1;
R(i,(lim>>1)+1,lim-1) W[i]=1ll*W[i-1]*tG%mod;
L(i,1,(lim>>1)-1) W[i]=W[i<<1];
}
void times(int *f,int *g)
{
static int sav[N<<1];
cpy(sav,f,lim);
NTT(sav,1,lim);NTT(g,1,lim);
px(g,sav,g,lim);NTT(g,0,lim);
R(i,0,lim-1) sav[i]=i>K?0:g[n-i];
NTT(sav,1,lim);
px(sav,t,sav,lim);NTT(sav,0,lim);
R(i,0,lim-1) sav[i]=i>K?0:sav[i];
reverse(sav,sav+K+1);
NTT(sav,1,lim);
px(sav,p,sav,lim);NTT(sav,0,lim);
R(i,0,lim-1) g[i]=(g[i]-sav[i]+mod)%mod;
clr(sav,lim);
}
signed main()
{
k=read(),m=read();
init(m<<1);n=(m-1)<<1;K=n-m;
R(i,1,m) p[i]=read_mod();
R(i,0,m-1) f[i]=read_mod();
p[0]=mod-1;
poly_inv(p,t,K);
NTT(t,1,lim);
reverse(p,p+m+1);NTT(p,1,lim);
a[1]=ans[0]=1;
while(k)
{
if(k&1) times(a,ans);
times(a,a);
k>>=1;
}
R(i,0,m-1) AN=(AN+1ll*ans[i]*f[i]%mod)%mod;
writeln(AN);
}
|
BZOJ 3625 小朋友与二叉树
(CF438E)
给定一棵$n$个节点的二叉树是合法的,当且仅当每个节点的权值都在给定的集合$C$中。对于每个$S\in [1,m]$,求有多少棵不同的,权值和为$S$的合法二叉树。
$n,m\leq 10^5$,$C$中的元素不超过$10^5$。
Sol:
令$f_s$表示满足条件的权重为$s$的二叉树数量
则有$f_0=1$
$$
f_s= \sum_{w\in {c_1,\ldots,c_n }}\sum_i f_i\times f_{s-w-i} (s>0)
$$
然后令$f$的普通生成函数为$F(x)=\sum\limits _{i=0}^{\infty} f_i x^i$
然后令$G(x)=\sum\limits_{i=1}^n x^{c_i}$
然后发现就有$F(x)=F(x)^2 G(x)+1$($+1$是因为$f_0=1$)
然后解得:
$$
f_s=\frac{1\pm \sqrt{1-4G(x)}}{2G(x)}
$$
然后由于$f_0=1,1\leq c_i$,所以取加号时并不可能。
所以有:
$$
f_s=\frac{1-\sqrt{1-4G(x)}}{2G(x)}=\frac{4G(x)}{2G(x)(1+\sqrt{1-4G(x)})}=\frac{2}{1+\sqrt{1-4G(x)}}
$$
然后就是多项式开根+求逆了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
const int N=333333;
const int _G=3;
const int invG=332748118;
int n,m;
int tr[N],tf;
inline void tpre(int n)
{
if(tf==n) return;tf=n;R(i,0,n-1) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
}
void NTT(int *g,int rev,int n)
{
tpre(n);
static ull f[N],w[N];w[0]=1;
R(i,0,n-1) f[i]=(((ll)mod<<5)+g[tr[i]])%mod;
for(int l=1;l<n;l<<=1)
{
ull tG=fpow(rev?_G:invG,(mod-1)/(l+l));
R(i,1,l-1) w[i]=w[i-1]*tG%mod;
for(int k=0;k<n;k+=l+l)
{
R(p,0,l-1)
{
int tt=w[p]*f[k|l|p]%mod;
f[k|l|p]=f[k|p]+mod-tt;
f[k|p]+=tt;
}
}
if(l==(1<<10)) R(i,0,n-1) f[i]%=mod;
}
if(!rev)
{
ull invn=fpow(n);
R(i,0,n-1) g[i]=f[i]%mod*invn%mod;
}
else R(i,0,n-1) g[i]=f[i]%mod;
}
void px(int *f,int *g,int *p,int n) {R(i,0,n-1)p[i]=1ll*f[i]*g[i]%mod;}
void poly_inv(int *f,int *g,int m)
{
int n=1;for(;n<m;n<<=1);
static int w[N],r[N],sav[N];
w[0]=fpow(f[0]);
for(int l=2;l<=n;l<<=1)
{
cpy(r,w,l>>1);
cpy(sav,f,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);clr(r,l>>1);
cpy(sav,w,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);
R(i,l>>1,l-1) w[i]=(w[i]*2ll-r[i]+mod)%mod;
}
cpy(g,w,m+1);clr(sav,n);clr(w,n);clr(r,n);
}
void poly_times(int *f,int *g,int *p,int n,int m,int lim)
{
static int tmpf[N],tmpg[N];
for(m+=n,n=1;n<m;n<<=1);
clr(tmpf,n),cpy(tmpf,f,n);
clr(tmpg,n),cpy(tmpg,g,n);
NTT(tmpf,1,n),NTT(tmpg,1,n);
px(tmpf,tmpg,p,n);NTT(p,0,n);
clr(p+lim,n-lim);clr(tmpf,n);clr(tmpg,n);
}
void poly_sqrt(int *f,int *g,int m)
{
int n=1;for(;n<m;n<<=1);
static int _g[N],ivg[N];
g[0]=1;
for(int l=2;l<=n;l<<=1)
{
R(i,0,(l>>1)-1) _g[i]=(g[i]<<1)%mod;
poly_inv(_g,ivg,l);
NTT(g,1,l);px(g,g,g,l);NTT(g,0,l);
R(i,0,l-1) g[i]=(f[i]+g[i])%mod;
poly_times(g,ivg,g,l,l,l);
}
clr(_g,n+n),clr(ivg,n+n);
}
int f[N],g[N],ivf[N];
signed main()
{
n=read(),m=read();
int x;
R(i,1,n) x=read(),g[x]++;
R(i,1,m) g[i]=mod-4ll*g[i]%mod;
g[0]=1;
poly_sqrt(g,f,m+1);
f[0]++;
poly_inv(f,ivf,m+1);
R(i,1,m) printf("%lld\n",2ll*ivf[i]%mod);
}
|
BZOJ 3684 大朋友与多叉树
定义一棵$n$个节点的树是合法的(无标号),当且仅当每个节点的孩子个数都在给定集合$C$中。求有多少棵不同的,叶节点为个数$S$的合法树。
$n,s\leq 10^5$,$C$中的元素不超过$10^5$。
首先令$f_n$表示叶节点个数为$n$的合法树的数量。
假如它有三个儿子,那么转移就是
$f_n+=\sum f_a\cdot f_b \cdot f_c,a,b,c\in C ,a+b+c=n$
令它的普通生成函数$F(x)$表示$F(x)=\sum\limits_{n=0}^{\infty} f_n x^n$
比如上面那个东西就是$F_3=F^3$($3$个$f$卷起来)
所以$F=\sum\limits_{c\in C}F^c+x$
其中这个$x$是因为刚刚只考虑了有孩子的情况,而没孩子就说明它自己就是叶子节点,此时就是$f$的边界情况$f_1=1$
然后令$G(\lambda)=\sum\limits_{c\in C} \lambda ^c$
然后就有$F(x)-G(F(x))=x$
然后再弄一个$H(\lambda)=\lambda$
然后就是$(H-G)(F(x))=x$
所以说$F(x)$就是$(H-G)$的复合逆,然后拉格朗日反演求出$(H-G)$的复合逆的第$n$项即可。时间复杂度一个$O(n \log n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
|
const int _G=7;
const int invG=135715694;
const int N=555555;
int n,m;
int tr[N],tf;
int f[N],g[N],inv[N];
inline void tpre(int n)
{
if(tf==n)return;tf=n;R(i,0,n-1) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
}
void NTT(int *g,int rev,int n)
{
tpre(n);
static ull f[N<<1],w[N<<1];w[0]=1;
R(i,0,n-1) f[i]=(((ll)mod<<5)+g[tr[i]])%mod;
for(int l=1;l<n;l<<=1)
{
ull tG=fpow(rev?_G:invG,(mod-1)/(l+l));
R(i,1,l-1) w[i]=w[i-1]*tG%mod;
for(int k=0;k<n;k+=l+l)
{
R(p,0,l-1)
{
int tt=w[p]*f[k|l|p]%mod;
f[k|l|p]=f[k|p]+mod-tt;
f[k|p]+=tt;
}
}
if(l==(1<<10)) R(i,0,n-1) f[i]%=mod;
}
if(!rev)
{
ull invn=fpow(n);
R(i,0,n-1) g[i]=f[i]%mod*invn%mod;
}
else R(i,0,n-1) g[i]=f[i]%mod;
}
void px(int *f,int *g,int *p,int n)
{
R(i,0,n-1) p[i]=1ll*f[i]*g[i]%mod;
}
void poly_inv(int *f,int *g,int m)
{
int n=1;for(;n<m;n<<=1);
static int w[N<<1],r[N<<1],sav[N<<1];
w[0]=fpow(f[0]);
for(int l=2;l<=n;l<<=1)
{
R(i,0,(l>>1)-1) r[i]=w[i];
cpy(sav,f,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);clr(r,l>>1);
cpy(sav,w,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);
NTT(r,0,l);
R(i,l>>1,l-1) w[i]=(w[i]*2ll-r[i]+mod)%mod;
}
cpy(g,w,m);clr(sav,n);clr(w,n);clr(r,n);
}
void poly_times(int *f,int *g,int *p,int n,int m,int lim)
{
static int tmpf[N<<1],tmpg[N<<1];
for(m+=n,n=1;n<m;n<<=1);
clr(tmpf,n);cpy(tmpf,f,n);
clr(tmpg,n);cpy(tmpg,g,n);
NTT(tmpf,1,n);NTT(tmpg,1,n);
px(tmpf,tmpg,p,n);NTT(p,0,n);
clr(p+lim,n-lim);clr(tmpf,n);clr(tmpg,n);
}
inline void poly_derivation(int *f,int *g,int n)
{
R(i,1,n-1)g[i-1]=1ll*f[i]*i%mod;g[n-1]=0;
}
inline void poly_integral(int *f,int *g,int n)
{
R(i,1,n-1)g[i]=1ll*f[i-1]*inv[i]%mod;g[0]=0;
}
void poly_mul(int *f,int *g,int *p,int n,int m)
{
for(m+=n,n=1;n<m;n<<=1);
NTT(f,1,n);NTT(g,1,n);
px(f,g,p,n);NTT(p,0,n);
}
void poly_ln(int *f,int *g,int n)
{
static int ff[N<<1],_f[N<<1],_g[N<<1];
poly_derivation(f,ff,n);
poly_inv(f,_f,n);
poly_times(ff,_f,_g,n,n,n);
poly_integral(_g,g,n);
clr(ff,n),clr(_g,n),clr(_f,n);
}
void poly_exp(int *f,int *g,int m)
{
if(m==1) {g[0]=1;return;}
static int s[N<<1],w[N<<1];
poly_exp(f,g,(m+1)>>1);
int n=1;
for(;n<(m<<1);n<<=1);
clr(s,m);
poly_ln(g,s,m);
tpre(n);
cpy(w,f,n);clr(w+m,n-m);
NTT(w,1,n);NTT(g,1,n);NTT(s,1,n);
R(i,0,n) g[i]=1ll*g[i]*(1-s[i]+w[i]+mod)%mod;
NTT(g,0,n);
clr(g+m,n-m);clr(s+m,n-m);clr(w+m,n-m);
}
void poly_fpow(int *f,int *g,int m,int k)
{
static int ff[N];
int n=1;for(;n<m;n<<=1);
poly_ln(f,ff,n);
R(i,0,n-1) ff[i]=1ll*ff[i]*k%mod;
poly_exp(ff,g,n);
}
int poly_lagrange_inversion(int *f,int m,int k)
{
static int g[N],ivf[N];
int n=1;for(;n<=m;n<<=1);
tpre(n);
poly_inv(f,ivf,n);
poly_fpow(ivf,g,n,k);
return 1ll*g[k-1]*inv[k]%mod;
}
inline void init_inv(int lim)
{
inv[1]=1;R(i,2,lim)inv[i]=1ll*inv[mod%i]*(mod-mod/i)%mod;
}
signed main()
{
init_inv(262144+5);
n=read(),m=read();
int x;
R(i,1,m) x=read(),g[x-1]=mod-1;//--g[x-1];
g[0]++,g[0]>=mod?g[0]-=mod:1;
writeln(poly_lagrange_inversion(g,n,n));
}
|
LOJ 2105 [TJOI2015] 概率论
对于一棵随机生成的$n$个节点的有根二叉树(所有互相不同构的形态等概率出现),求叶子节点数的期望。
$n\leq 10^9$。同构的判定如下:
sol:
假如说是求这样的二叉树的个数,那么就是卡特兰数。
所以期望=叶子数和/树个数,然后令叶子数和为$f_n$,树个数为$g_n$,而$g_n$是卡特兰数。
然后现在来求$f_n$,就枚举两边儿子大小:
先枚举左边儿子大小$i$,方案数为$\sum f_i \cdot g_{n-i-1}$,然后再枚举右边儿子大小$i$,方案数同样为$\sum f_i \cdot g_{n-i-1}$
所以说$f_n=2 \sum\limits_{i=0}^{n-1} f_i \cdot g_{n-i-1}(n>1)$
而只有一个节点时$f_1=1$
然后这又是一个卷积的形式
令$f$的普通生成函数为$F(x)$,$g$的普通生成函数为$G(x)$
$$
F(x)-x=\sum_{n=2}^{\infty} f_n x^n= 2\sum_{n=2}^{\infty} \sum_{i=0}^n f_i \cdot g_{n-i-1} x^n
$$
令$j=n-i-1$
$$
=2\sum_{i=0}^n f_ix^i \sum_{j=1}^{\infty} g_j x^j x
$$
所以
$$
F(x)=2\cdot F(x) G(x)x+x
$$
$2\cdot F(x)G(x)$旁边乘$x$是因为上面是$g_{n-i-1}$,然后$+x$则是$n=1$时的情况。
其中$G(x)=\frac{1-\sqrt{1-4x}}{2x}$
然后把$G(x)$代回去,就有$F(x)=\frac{x}{\sqrt{1-4x}}$
然后假如现在知道$g$,求$f$。
考虑怎么把$\sqrt{1-4x}$从分子搞到分母上
左边是$G$所以可以搞出$(1-4x)^{\frac{1}{2}}$这一项,然后通过这个求右边的$x(1-4x)^{-\frac{1}{2}}$
具体地:
对这个$(1-4x)^{\frac{1}{2}}$求导,得到:$-2\cdot (1-4x)^{-\frac{1}{2}}$
然后代回去,那么$2x\cdot G(x)=1-\sqrt{1-4x}$
然后对它求导$(2x\cdot G(x))'=2(1-4x)^{-\frac{1}{2}}=\frac{2}{x}\cdot F$
所以$F=x\cdot (x\cdot G(x))'$
而我们只需要求
$$
f_n= [x^n] F(x)=[x^n]x\cdot (x\cdot G(x))'
$$
$$
=[x^{n-1}] (x\cdot G)'=n[x^{n-1}]G(x)
$$
所以
$$
\frac{f_n}{g_n}=\frac{g_{n-1}\cdot n}{g_n}
$$
而$g_n=\frac{1}{n+1} \binom {2n} {n}$
所以$\frac{f_n}{g_n}=\frac{n(n+1)}{4n-2}$
这个题就做完了。
时间复杂度$O(1)$。
UOJ #50链式反应
求满足下列条件的$n$个点的带标号树的个数:
- 父亲的编号大于儿子。
- 一个点如果有儿子,则有两个无序的$\alpha$型儿子,有$c$个无序的$\beta$型儿子,其中$c\in A$。
- 如果一个点是根节点或$\alpha$型儿子,那么它可以有儿子或者是叶节点;如果一个点是$\beta$型儿子,那么它只能是叶节点。
对于所有的$n\leq n_{\max}$求出答案。
$n_{\max}\leq 2\times 10^5$。
首先考虑$dp$。
令$f_n$表示$n$个节点的方案数。首先有$f_1=1$。
考虑枚举两个$\alpha$型儿子的子树大小分别为$j,k$,剩下就是$\beta$型。于是要满足$i-j-k-1 \in A$。
然后考虑先选出两个$\alpha$型儿子的编号,方案数为$\binom {i-1} {j} \cdot \binom {i-1-j} {k}$。然后将两个子树的节点都重标号,方案数为$f_j$和$f_k$。
所以有
$$
f_i =\frac{1}{2} \sum_j \sum_k \binom {i-1}{j} \binom {i-1-j}{k} f_j f_k [i-j-k-1 \in A]
$$
首先有$\binom {i-1}{j} \binom{i-j-1} {k} =\frac{(i-1)!}{j!k!(i-j-k-1)!}$
然后考虑枚举$i+j$的和:
$$
f_i= \frac{1}{2} \sum_s [i-s-1 \in A]\frac{(i-1)!}{(i-s-1)!} \sum_{j=0}^s \frac{f_j}{j!} \frac{f_{s-j}}{(s-j)!}
$$
然后将$\sum_{i=0}^s \frac{f_i}{i!} \frac{f_{s-i}}{(s-i)!}$记作$g_x$。
然后这又是一个卷积的形式。
这样直接做是$O(n^2)$的。
而因为$g$依赖于$f$,而$f$又依赖于$g$。
然后就要用到一个叫分治FFT的东西。
假设要求$f_{l,\ldots r}$的值。
那将它分前一半,后一半,然后先求出前一半。
那么假设现在要求$f_i$的值,将它写成$g$和$h$的卷积
$$
f_i=(i-1)! \sum_{j+k=i-1} g_j h_k
$$
现在因为$h$一开始就知道,可以先求出来,现在将$j$分个类。
考虑分治的过程中包含$i$的区间,然后$j$的取值一定要在$i$的左边。
对于分治过程中的对于右半边的每一个$i$,考虑左半边的每一个$j$对他的贡献,然后只要将这几个区间加起来就得到了他们的贡献。
把$j$那一段拿出来,再把$k$一段拿出来卷一下,就得到了左边对右边的贡献,再找出对应的位置就好了。
时间复杂度$O(n\log^2 n)$
然后卡常就可以过了…
标算是$O(n\log n)$了…
https://vfleaking.blog.uoj.ac/blog/43
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
const int _G=3;
const int invG=332748118;
int m,n;
char s[444444];
int F[888888],G[888888],G2[888888];
int fac[888888],inv[888888],Finv[888888];
int s1[888888],s2[888888],s3[888888];
inline void init_FAC(int lim)
{
fac[0]=Finv[0]=inv[1]=1;
R(i,2,lim) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
R(i,1,lim) fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
// R(i,1,lim) printf("%lld %lld %lld\n",fac[i],inv[i],Finv[i]);
}
int tr[888888],tf;
void tpre(int n)
{
if(tf==n) return;tf=n;
R(i,0,n-1) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
}
void NTT(int *g,int rev,int n)
{
tpre(n);
static ull f[888888],w[888888];w[0]=1;
R(i,0,n-1) f[i]=(((ll)mod<<5)+g[tr[i]])%mod;
for(int l=1;l<n;l<<=1)
{
ull tG=fpow(rev?_G:invG,(mod-1)/(l+l));
R(i,1,l-1) w[i]=w[i-1]*tG%mod;
for(int k=0;k<n;k+=l+l)
{
R(p,0,l-1)
{
int tt=w[p]*f[k|l|p]%mod;
f[k|l|p]=f[k|p]+mod-tt;
f[k|p]+=tt;
}
}
if(l==(1<<10)) R(i,0,n-1) f[i]%=mod;
}
if(!rev)
{
ull invn=fpow(n);
R(i,0,n-1) g[i]=f[i]%mod*invn%mod;
}
else R(i,0,n-1) g[i]=f[i]%mod;
}
void px(int *f,int *g,int *p,int n) {R(i,0,n-1)p[i]=1ll*f[i]*g[i]%mod;}
void cdq(int l,int r)
{
//printf("%lld %lld\n",l,r);
//printf("G:"); R(i,0,n-1) printf("%lld ",G[i]);puts("");
if(r==1) return;
if(r-l==1) {if(l!=1)G[l]=1ll*G[l]*fpow(2*l)%mod;return;}
int mid=(l+r)>>1,n=r-l,nd2=n/2;
cdq(l,mid);
if(l==0)
{
cpy(s1,G,nd2);clr(s1+nd2,nd2);NTT(s1,1,n);
px(s1,s1,s1,n);NTT(s1,0,n);
R(i,nd2,n-1) G2[i]=(G2[i]+s1[i])%mod;
cpy(s1,G2,nd2);clr(s1+nd2,nd2);NTT(s1,1,n);
cpy(s2,F,nd2);clr(s2+nd2,nd2);NTT(s2,1,n);
px(s1,s2,s1,n);NTT(s1,0,n);
R(i,nd2,n-1) G[i]=(G[i]+s1[i])%mod;
}
else
{
cpy(s1,G+l,nd2);clr(s1+nd2,nd2);NTT(s1,1,n);
cpy(s2,G,n);NTT(s2,1,n);
px(s1,s2,s1,n);NTT(s1,0,n);
R(i,nd2,n-1) G2[i+l]=(G2[i+l]+2ll*s1[i])%mod;
cpy(s1,F+l,nd2);clr(s1+nd2,nd2);NTT(s1,1,n);
cpy(s2,G2,n);NTT(s2,1,n);
px(s1,s2,s1,n);
cpy(s3,s1,n);
cpy(s1,G2+l,nd2);clr(s1+nd2,nd2);NTT(s1,1,n);
cpy(s2,F,n);NTT(s2,1,n);
px(s1,s2,s1,n);
R(i,0,n-1) s3[i]=(s3[i]+s1[i])%mod;
NTT(s3,0,n);
R(i,nd2,n-1) G[i+l]=(G[i+l]+s3[i])%mod;
}
cdq(mid,r);
}
signed main()
{
m=read();scanf("%s",s+1);
init_FAC(m+10);
G[1]=1;
R(i,1,m) if(s[i]=='1') F[i]=Finv[i-1];
for(n=1;n<=m;n<<=1);
cdq(0,n);
R(i,1,m) writeln(1ll*fac[i]*G[i]%mod);
}
|
HDU6585
求无标号,有根,连通,且每条边在恰好一个环的无向图个数。
$n\leq 10^5$。
考虑把根去掉之后会得到一串,考虑一串上面挂的方式。
令$a_n$是有根仙人掌的个数(将$n-1$个点丢进任意个连通块的方案数),然后根节点上会连很多个环,且每一个环是独立的。
将根节点断开会形成很多个连通块,每一块分别考虑。
由于每条边在且仅在一个环内,所以一个连通块应该长成某个点从根节点进来,然后中间连出一个环,再从某个点出去。
然后在这个链上挂了若干个仙人掌。
然后把这些边也砍了,分别看。
因为现在假如已经定了这样一个根,然后就可以定下来这么一个链,这些仙人掌都相当于有根,然后将根挂在这个链上。
设$b_n$表示环上一共有$n$个点,$b_n=a_n+\sum\limits_{i=1}^{n-1} a_i b_{n-i}$。
这是不考虑重复时的方案数。
但是有些这样的会算两遍:

一个naive的想法是直接给它除个二,但是这样会算少。
比如这样子的,翻了之后还是自己,但是这本身就只算了一次。

所以考虑处理出来回文的有多少个,然后除的时候去掉。
然后挂着的点数分奇偶考虑:
偶数的话就是直接算一半,然后另一半对着复制过去即可。即$b_{\frac{n}{2}}$
而假如挂了奇数个点:
那么不仅要把前一半翻过去,还要枚举中间一个。
然后考虑递推,假设方案数为$c_n=a_n+\sum\limits_{i=1}^{\lfloor \frac{n}{2}\rfloor } a_i c_{n-2i}$
令$d_n$表示环上只挂了一个大小为$n$的连通块的内部连边方案数
最后答案为$d_n=\frac{1}{2} (b_n+c_n+b_{\frac{n}{2}})$
然后再来考虑$a_n$是什么,就相当于要搭配一个东西,可以往里面随便塞东西,每一个大小的东西有不同的样式(连通块内部连接方式),大小为$n$的样式个数为$d_n$。且由于没有标号,假如大小为$3$有红的和绿的,那么放两个红的和一个绿的与先放一个红的再放一个绿的再放一个红的是一样的。
考虑用生成函数的思想来做
对于$n$个点有$d_n$种样式,对于每一种样式,枚举它选了多少个,假如选了$k$个,然后就相当于每一个样式的生成函数卷积起来,是一个背包。
$$
[x^m]\prod_{n=1}^{\infty} \prod_{i=1}^{d_n} \sum_{k=0}^{\infty} 1\cdot x^{nk}
$$
这里$nk$指$nk$个点。
而这个的$m$次项就代表$m$个点分到若干个连通块的方案数。
$a_n$表示把$n-1$个点分进这些连通块的方案数
$$
\sum_{n=1}^{\infty} a_n x^n= x\prod _{i=1}^{\infty} \prod_{j=1}^{d_i} \sum_{k=0}^{\infty} x^{ik}
$$
$$
\sum_{n=1}^{\infty} a_n x^{n-1}=\prod _{i=1}^{\infty} \prod_{j=1}^{d_i} \sum_{k=0}^{\infty} x^{ik}
$$
$$
\sum_{n=1}^{\infty} a_n x^{n-1}=\prod _{i=1}^{\infty} \big(\sum_{k=0}^{\infty} x^{ik}\big) ^{d_i}
$$
将$\sum\limits_{k=0}^{\infty} x^{ik}$单独拿出来,拆开,发现这是一个等比数列:
$$
\sum_{k=0}^{\infty} x^{ik} = \sum_{k=0}^{\infty} (x^i)^k =\frac{1}{1-x^i}
$$
$$
\sum_{n=1}^{\infty} a_n x^{n-1}=\prod _{i=1}^{\infty} \frac{1}{(1-x^i)^{d_i}}
$$
然后两边取$\ln$
$$
\ln \sum_{n=1}^{\infty} a_n x^{n-1} = \sum_{i=1}^{\infty} \ln \frac{1}{(1-x^i)^{d_i}}=\sum_{i=1}^{\infty} -\ln (1-x^i)^{d_i}=\sum_{i=1}^{\infty} d_i \cdot \big(-\ln (1-x^i)\big)
$$
然后因为$-\ln(1-x)=\sum\limits_{i=1}^{\infty} \frac{x^i}{i}$
所以:
$$
\ln \sum_{n=1}^{\infty} a_n x^{n-1}= \sum_{i=1}^{\infty} d_i \sum_{j=1}^{\infty}\frac{x^{ij}}{j}
$$
然后求个导($\frac{\mathrm{d}(\ln A)}{\mathrm{d} x}=\frac{A'}{A}$):
$$
\frac{\mathrm{d}\ln \sum\limits_{n=1}^{\infty}a_n x^{n-1}}{\mathrm{d} x}=\frac{\mathrm{d}\sum\limits_{i=1}^{\infty}d_i \sum\limits_{j=1}^{\infty}\frac{x^{ij}}{j}}{\mathrm{d} x}
$$
$$
\frac{\sum\limits_{n=2}^{\infty}(n-1)a_n x^{n-2}}{\sum\limits_{n=1}^{\infty}a_n x^{n-1}}=\sum_{i=1}^{\infty} d_i \sum_{j=1}^{\infty} \frac{ijx^{ij-1}}{j}=\sum_{i=1}^{\infty}i\cdot d_i \sum_{j=1}^{\infty} x^{ij-1}
$$
$$
\sum_{n=2}^{\infty} (n-1)a_n x^{n-2} =\sum_{n=1}^{\infty} a_n x^{n-1}\big(\sum_{i=1}^{\infty} i \cdot d_i\sum_{j=1}^{\infty} x^{ij-1} \big)
$$
$$
\sum_{n=2}^{\infty} (n-1)a_n x^{n} =\sum_{n=1}^{\infty} a_n x^{n}\big(\sum_{i=1}^{\infty} i \cdot d_i\sum_{j=1}^{\infty} x^{ij} \big)
$$
然后将$\sum\limits_{i=1}^{\infty} i\cdot d_i \sum\limits_{j=1}^{\infty} x^{ij}$提出来,令$k=ij$考虑枚举$k$,则原式化为:
$$
\sum_{k=1}^{\infty} \big(\sum_{i|k} i\cdot d_i \big)x^k
$$
那么假如已知$d_i$,算$\sum\limits_{i|k} i\cdot d_i$就是$\log n$的,然后假设这个为$e_k$。
那么
$$
\sum_{n=2}^{\infty}(n-1) a_n x^n =\big(\sum_{n=1}^{\infty} a_n x^n \big) \big(\sum_{k=1}^{\infty} e_k x^k \big)
$$
把右边卷出来之后把左边的$n-1$除掉,就又得到了$a_n$。
而假如知道$a_i$就可以算出$b_i$和$c_i$,而已知$b_i$和$c_i$又可以算出$d_i$,知道$d_i$就可以算出$\sum\limits_{i|k} i\cdot d_i$,然后就可以算出$a_i$,分治FFT即可。
时间复杂度$O(n\log^2 n)$
LOJ 6569 仙人掌计数
对于所有$i\in[1,n]$,求有多少个$i$个节点的有标号仙人掌。
$n\leq 3\times 10^4$。
令$1$号点为根,还是考虑一个根会对应好多个环,但这边无所谓:
考虑有$c$和$d$的卷积,$a_n=\sum\limits_{i=0}^n\binom n i c_i d_{n-i}$
所以就有
$$
\frac{a_n}{n!}=\sum_{i=0}^n \frac{c_i}{i!} \frac{d_{n-i}}{(n-i)!}
$$
然后写成指数生成函数的形式
$$
\hat{A} =\hat{C} \hat{D}
$$
那比如现在有很多个连通块,现在要算每一个连通块内部的方案数,比如不包括根节点环长是$i$
,假如现在有$3$个点,那现在相当于要$3$个分别搞一个图出来,保证各自内部标号顺序不变,然后再叉起来。
一个例子:
比如现在有两个子树长成这个样子。
新的节点肯定为1号节点,那么其他节点可以长这个样子。
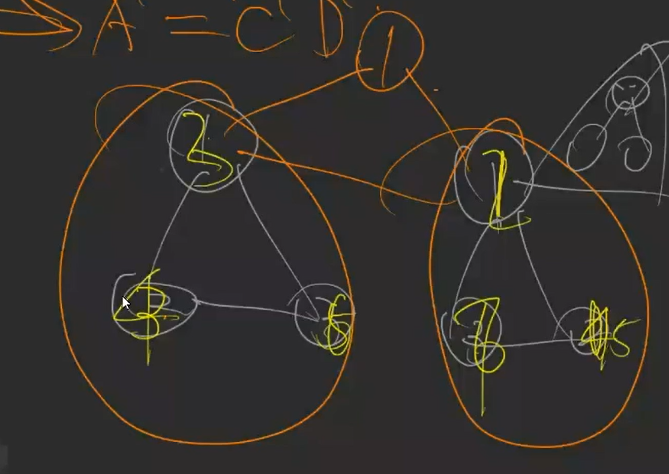
设左边的大小为$S_1$,右边的大小为$S_2$,总点数为$n$,$a$内部连边方案数
然后这样两个东西卷起来的方案数为:
$$
\binom {n} {S_1}\times a_{S_1} a_{S_2}
$$
这个东西就刚刚上面说的那种卷积。
那么挂$i$个连通块的方案数就是$(\hat{F})^i$
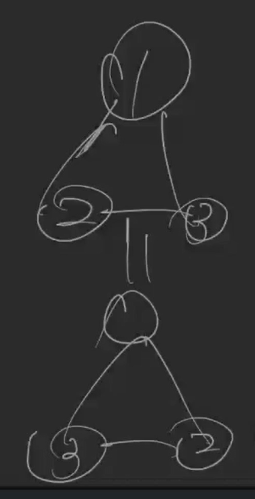
但是像这两种仍然是同一种方案。因为每一个点连的都一样。
所以这个也要环翻转的问题,但理由是不一样的。
刚刚是因为没有标号所以环翻转之后看形态
而这个是因为我们已经标好号了,但并不知道怎么去数第一个子树,第二个子树……我们有可能会正着数,也有可能会倒着数。
有可能但现在这个只要直接除以$2$即可,因为已经确定形状就算是回文的也有两种标号方式。
然而在$i=1$时不变。。
那么一个子仙人掌的方案数就是:
$$
\hat{F}(x)+\sum_{k\ge 2} \frac{1}{2}\big(\hat{F}(x)\big )^k
$$
然后来考虑有多个连通块怎么办:
考虑将根节点去掉之后可以分成若干个不交的子仙人掌,而且是有标号问题,因此去掉根节点之后,方案数就是:
$$
\exp\left( \hat{F}(x)+\sum_{k\ge 2} \frac{1}{2}\big(\hat{F}(x)\big )^k\right)
$$
而里面的$\sum\limits_{\ge 2} \frac{1}{2}\big(\hat{F}(x) \big)^k$是一个等比数列的形式,所以原式可以化为:
$$
\exp \left(\frac{2\hat{F}(x)-\big(\hat{F}(x) \big)^2}{2-2\hat{F}(x)}\right)
$$
总的是$\hat{F}(x)$,而去掉根节点之后是$\exp \left(\frac{2\hat{F}(x)-\big(\hat{F}(x) \big)^2}{2-2\hat{F}(x)}\right)$
所以
$$
\hat{F} (x)=x\cdot \exp \left(\frac{2\hat{F}(x)-\big(\hat{F}(x) \big)^2}{2-2\hat{F}(x)}\right )
$$
这是一个方程,所以牛顿迭代即可
令:
$$
f(\hat{F})= x\cdot \exp \left(\frac{2\hat{F}-\big(\hat{F} \big)^2}{2-2\hat{F}}\right) -\hat{F} =0
$$
$$
f'(\hat{F})=x\left(\exp(\frac{2\hat{F}-\big(\hat{F}\big)^2}{2-2\hat{F}})\right)'-1
$$
$$
=x\exp \left(\frac{2\hat{F}-\hat{F}^2}{2-2\hat{F}} \right) \left(\frac{2\hat{F}-\hat{F}^2}{2-2\hat{F}}\right)'-1
$$
$$
=x \exp \left(\frac{2\hat{F}-\hat{F}^2}{2-2\hat{F}} \right)\left(\frac{(2-2\hat{F})^2- (-2)\left(2\hat{F}-\hat{F}^2 \right)}{\left(2-2\hat{F}\right)^2} \right)-1
$$
$$
=x \exp \left(\frac{2\hat{F}-\hat{F}^2}{2-2\hat{F}} \right) \left(1+\frac{4\hat{F}-2\hat{F}^2}{(2-2\hat{F} )^2} \right)-1
$$
$$
\hat{T_1}(x)=\hat{F}(x)-\frac{f\left(\hat{F}(x)\right)}{f'\left(\hat{F}(x) \right)}=\hat{F}(x)-\frac{2x \exp\left(\frac{2\hat{F}(x)-\hat{F}(x)^2}{2-\hat{F}(x)} \right)-2\hat{F}(x)}{x\exp \left(\frac{2\hat{F}(x)-\hat{F}(x)^2}{2-\hat{F}(x)} \right)\left(1+\frac{1}{(\hat{F}(x)-1)^2} \right) -2}
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
|
const int N=555555;
const int _G=3;
const int invG=fpow(_G);
int fac[N],Finv[N],inv[N];
inline void init(int lim=262144)
{
inv[1]=Finv[0]=fac[0]=1;
R(i,2,lim) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
R(i,1,lim) fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
//R(i,1,10) printf("fac:%lld inv:%lld FInv:%lld\n",fac[i],inv[i],Finv[i]);
}
int tr[N],tf;
void tpre(int n)
{
if(tf==n) return;tf=n;
int ndiv2=n>>1;
R(i,0,n+5) tr[i]=(tr[i>>1]>>1)|((i&1)?ndiv2:0);
}
void NTT(int *g,int rev,int n)
{
tpre(n);
static ull f[N],w[N];w[0]=1;
R(i,0,n-1) f[i]=g[tr[i]]%mod;
for(int l=1;l<n;l<<=1)
{
ull tG=fpow(rev?_G:invG,(mod-1)/(l+l));
R(i,1,l-1) w[i]=w[i-1]*tG%mod;
for(int k=0;k<n;k+=l+l)
{
R(p,0,l-1)
{
int tt=w[p]*f[k|l|p]%mod;
f[k|l|p]=f[k|p]+mod-tt;
f[k|p]+=tt;
}
}
if(l==(1<<10)) R(i,0,n-1) f[i]%=mod;
}
if(!rev)
{
int invn=fpow(n);
R(i,0,n-1) g[i]=f[i]%mod*invn%mod;
}
else R(i,0,n-1) g[i]=f[i]%mod;
}
inline void px(int *f,int *g,int *p,int n) {R(i,0,n-1)p[i]=1ll*f[i]*g[i]%mod;}
void poly_times(int *f,int *g,int *p,int n,int m,int lim)
{
static int tmpf[N],tmpg[N];
for(m+=n,n=1;n<m;n<<=1);
clr(tmpf,n);cpy(tmpf,f,n);NTT(tmpf,1,n);
clr(tmpg,n);cpy(tmpg,g,n);NTT(tmpg,1,n);
px(tmpf,tmpg,p,n);NTT(p,0,n);
clr(p+lim,n-lim);
clr(tmpf,n);clr(tmpg,n);
}
void poly_mul(int *f,int *g,int *p,int n)
{
static int tmpf[N],tmpg[N];
int m=n<<1;
clr(tmpf,m);cpy(tmpf,f,m);NTT(tmpf,1,m);
clr(tmpg,m);cpy(tmpg,g,m);NTT(tmpg,1,m);
px(tmpf,tmpg,p,m);
NTT(p,0,m);
clr(tmpf,m),clr(tmpg,m);
}
void poly_inv(int *f,int *g,int m)
{
int n=1;for(;n<m;n<<=1);
static int w[N],r[N],sav[N];
w[0]=fpow(f[0]);
for(int l=2;l<=n;l<<=1)
{
cpy(r,w,l>>1);NTT(r,1,l);
cpy(sav,f,l);NTT(sav,1,l);
px(r,sav,r,l);NTT(r,0,l);clr(r,l>>1);
cpy(sav,w,l);NTT(sav,1,l);
NTT(r,1,l);px(r,sav,r,l);NTT(r,0,l);
R(i,l>>1,l-1) w[i]=(2ll*w[i]-r[i]+mod)%mod;
}
cpy(g,w,m);clr(sav,n);clr(w,n);clr(r,n);
}
inline void poly_derivation(int *f,int *g,int n)
{
R(i,1,n-1) g[i-1]=1ll*f[i]*i%mod;g[n-1]=0;
}
inline void poly_integral(int *f,int *g,int n)
{
R(i,1,n-1) g[i]=1ll*f[i-1]*inv[i]%mod;g[0]=0;
}
void poly_ln(int *f,int *g,int n)
{
static int ff[N],_f[N],_g[N];
poly_derivation(f,ff,n);
poly_inv(f,_f,n);
poly_times(ff,_f,_g,n,n,n);
poly_integral(_g,g,n);
clr(ff,n),clr(_f,n),clr(_g,n);
}
void poly_exp(int *f,int *g,int m)
{
static int s[N],s2[N],w[N];
int n=1;for(;n<m;n<<=1);
clr(g,n<<1);
s2[0]=1;
for(int l=2;l<=n;l<<=1)
{
cpy(s,s2,l>>1);poly_ln(s,s,l);
cpy(w,s2,l);
R(i,0,l-1) s[i]=(f[i]-s[i]+mod)%mod;
s[0]=(s[0]+1)%mod;
poly_times(s2,s,s2,l,l,l);
}
cpy(g,s2,m);clr(s,n);clr(s2,n);clr(w,n);
}
int F[N],G1[N],G2[N],G[N],G3[N];
void newton(int *f,int n=262144)
{
if(n==2) {f[1]=1;return;}
newton(f,n>>1);
poly_times(f,f,G1,n,n,n);
//2F-F^2
R(i,0,n-1) G1[i]=(f[i]+f[i]-G1[i]+mod)%mod,G2[i]=(mod-f[i]-f[i]+mod+mod)%mod;
G2[0]+=2;G2[0]>=mod?G2[0]-=mod:1;//2-2F
cpy(G3,G2,n);
poly_inv(G3,G2,n);// 1/(2-2F)
poly_times(G1,G2,G1,n,n,n);// (2F-F^2)/(2-2F)
cpy(G3,G1,n);
poly_exp(G3,G1,n);//exp((2F-F^2)/(2-2F))
L(i,1,n-1) G1[i]=G1[i-1];
G1[0]=0;//x*exp((2F-F^2)/(2-2F))
R(i,0,n-1) G[i]=(G1[i]+G1[i]-f[i]-f[i]+mod+mod)%mod;//2x*exp((2F-F^2)/(2-2F))-2F
cpy(G2,f,n);
G2[0]+=(mod-1),G2[0]>=mod?G2[0]-=mod:1;//F-1
poly_times(G2,G2,G2,n,n,n);//(F-1)^2
poly_inv(G2,G2,n);//1/((F-1)^2)
G2[0]++,G2[0]>=mod?G2[0]-=mod:1;//1/((F-1)^2) +1
poly_times(G1,G2,F,n,n,n);//x*(exp((2F-F^2)/(2-2F)))*(1/((F-1)^2) +1)
F[0]+=(mod-2),F[0]>=mod?F[0]-=mod:1;//x*(exp((2F-F^2)/(2-2F)))*(1/((F-1)^2) +1)-2
poly_inv(F,F,n);
poly_times(G,F,G,n,n,n);
R(i,0,n-1) f[i]=(f[i]-G[i]+mod)%mod;
}
int f[N],x;
signed main()
{
init();
newton(f);
for(int _=read();_;_--)
{
x=read();
writeln(1ll*f[x]*fac[x-1]%mod);
}
}
|
时间复杂度$O(n\log n)$
HDU 6426 烷烃计数
给定$n$,求$n$个点无标号的,每个节点度数$\leq 4$的无根树个数,以及还要求根节点度数$\leq 3$的无根树个数。
$n,T\leq 10^5$
咕咕咕






