问题引入

给定有向带权图，两个点$s$和$t$，求$s\to t$的最小割是否唯一。（CF gym 100200A）

对于每条边，判断是否可能在最小割中？

是否一定在最小割中？

之后会讲怎么给出一个最小割的方案以及与2-SAT之间的关系，从而更本质地去揭示最小割的结构与性质。

网络流的定义

$f(u,v)$表示$u$到$v$的流量，满足$f(v,u)=-f(u,v)$

$c(u,v)$表示$u$到$v$的最大流量限制，满足$f(u,v)\leq c(u,v)$

对于除去源点$s$和汇点$t$以外的$u$，满足流量平衡限制：$\sum f(u,x)=0$

（假设$f(s,t)=0$）

网络流的性质

$$ \sum f(s,x)=\sum f(x,t) $$

证明：

假设$f(s,t)=0$

令$S=V-{s}-{t}$由流量平衡限制可以得出： $$ \sum_{x\in S} \sum_{y\in V} f(x,y)=0 $$ 因为右边这些等于零，所以$S$里面流量之和也是等于零。

然后将这些边分成$x,y\in S$和 $x\in S$而$y\notin S$，所以就有： $$ \sum_{x\in S,y\in S} f(x,y)+\sum_{x\in S} f(x,s)+f(x,t)=0 $$ 对于左边，由于对于任何一对$f(x,y)$出现就一定会有$f(y,x)$出现，由于$f(x,y)+f(y,x)=0$，所以左边为零。

对于右边，由于$f(x,s)=-f(s,x)$所以整理就可以获得 $$ \sum_{x\in S} f(x,t)=\sum_{x\in S} f(s,x) $$ 记$\operatorname{value}(f)$为网络流的流量，记某集合$S$包含源点$s$，且不包含汇点$t$，那么： $$ \operatorname{value}(f)=\sum _{x\in S,y\notin S} f(x,y) $$ 大概就是将上面的证明将$s$放到$S$中

原来是 $$ \sum_{x\in S} \sum_{y\in V} f(x,y)=0 (s\notin S) $$ 那么就会多出$\sum f(s,x)$的流量。

所以： $$ \operatorname{value}(f)=\sum _{x\in S,y\notin S} f(x,y) $$

最大流-最小割定理

s-t​割的定义

$S$和$T$是$V$的一个划分（$S\cap T ={},S\cup T=V$），且$S$包含$s$，$T$包含$t$。

定义$c(S,T)=\sum\limits_{x\in S \and y\in T} c(x,y)$ $$ \operatorname{value}(f)\leq c(S,T) $$ 证明：

根据上面的性质可以得到 $$ \sum_{x\in S,y\in T} f(x,y)=\operatorname{value}(f) $$ 且$f(x,y)\leq c(x,y)$

所以就是 $$ \operatorname{value}(f)=\sum_{x\in S,y\notin S} f(x,y)\leq \sum c(x,y)=c(S,T) $$ 以及另一种割的定义：

割是边集的一个子集，满足从原图中删去割中的边则$s\to t$不连通。割的权值为割边权值之和。

之前定义的s-t割属于这种割。

证明：这种定义的割的最小权值不会小于之前定义的s-t割的最小权值。因为这种广义的割就是在s-t割的基础上多割一些边。

接下来只考虑s-t割。

s-t的最大流的值与s-t最小割的值相同。

（线性规划中对偶定理的一个特殊情况）

在证明之前先讲一下残余网络：

残余网络

$r(u,v)=c(u,v)-f(u,v)$

只考虑$r(u,v)>0$的边

增广路径：残余网络中的每条边的$r$都大于$0$。

ford-fulkerson算法：沿增广路径增广直到不存在增广路径。

所以说这么一直增广下去一定会存在一个增广状态不存在增广路径了。

因此考虑残余网络上$s$能到达的点集$S$，设$T=\frac{V}{S}$。

那么一定有$c(S,T)=\operatorname{value}(f)$

此时一定满足最大流=最小割

最小割的条件

对于任意最大流$f$，s-t割$(S,T)$为最小割当且仅当对于任意割边$(u,v)$都有$r(u,v)=0$。

$$ c(S,T)=\sum c(x,y)=\sum f(x,y)+r(x,y) $$ 因为$\sum f(x,y)$是最大流与$c(S,T)$流的流量相同。

所以$\sum r(x,y)=0$，因此$\forall x\in S,y\in T,r(x,y)=0$

原图最小割当且仅当残余图的最小割，因为残余图任意的割的值都$\ge 0$，因此残余图中的最小割每条边都是$0$。

所以最小割的充要条件为：$s$在$S$中，$t$不在$S$中，对于所有$r(u,v)>0$，$u$在$S$中则$v$也要在$S$中。

举个例子：

这样一张图，每一条边的流量为1，最大流长这个样子：

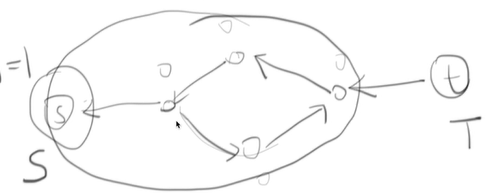
那么它的残余网络长这个样子：

注意这里的每一条有向边$(u,v)$就表示$r(u,v)=1$

具体原因为如图中$c(s,1)=1,c(1,s)=0$。

而$f(s,1)=1,f(1,s)=-1$所以$r(s,1)=0,r(1,s)=1$。

比如存在一条$u\to v$的边，$u$在$S$中必定$v$会在$S$中。

然后考虑找出残余网络中的最小割。

要么是只有$s$自己，要么是$s$和中间这一堆。

那么这在原图中对应就是

这其实是一个2-SAT的模型。

$x_i=[i\in S],x_s=true,x_t=false$

$\forall r(u,v)>0 ,x_u=true \to x_v=true,x_v=false \to x_u=false$

因此判断是否是最小割被转化为一个2-SAT的问题。

最小割解集$\ge$2-SAT解集。

这里的2-SAT并不需要真正地把图建出来然后再去跑，可以用以下算法取判断：

最小割的2-SAT结构：

三种标记：未标记、必定在$S$中，必定在$T$中，记为0, S, T。

点限制：

$x$在$S$中：将$x$能到达的点都标记为$S$

$x$在$T$中：将能到达$x$的点都标记为$T$

边限制转化为点限制：

$(u,v)$在s-t最小割中：$u$在$S$中，$v$不在$T$中

判断2-SAT是否合法就只需要判断是否有一个点是否同时被标记为$S$且同时被标记为$T$。

即判断当前限制下是否存在最小割：不存在某个点被同时标记为$S$和$T$。

而判断当前限制下最小割是否唯一：不存在0标记的点。

比如刚刚那个例子：

pic1.png

初始有两个限制$s\in S,t\in T$，所以就把$s$标记成$S$，把$t$标记成$T$，不过源点没有任何能到达的点，也没有任何能到达汇点的点，所以剩下的点都是未标记的点。

那么发现对于任意情况将所有未标记的点全标记成$S$或$T$都是合法的。

例题应用

判断$(u,v)$是否可能在s-t最小割中？

判断$(u,v)$是否一定在s-t最小割中？

通过以上分析就可以不用网络流的视角去想这两个问题，可以直接跳过网络流直接用2-SAT去做。

（2-SAT有一个性质：如果一个方程有解，然后新加入一些$x,y,z$的限制，只需要判断$x,y,z$三个变量之间会不会矛盾即可）

判断$(u,v)$是否可能在s-t最小割中？

经典做法：

将$(u,v)$权值减少eps，检查最小割是否变小

若$r(u,v)>0$，则最小割一定不会变小

若$r(u,v)=0$，则等价于能否退流，即是否存在$u\to v$的增广路径。

2-SAT做法：

$u$设为$S$，$v$设为$T$且不合法$\to $存在$u\to v $的增广路径。

判断$(u,v)$是否一定在s-t最小割中？

经典做法：

将$(u,v)$权值增加eps，检查最小割是否变大

最小割变大$\to$最大流增加，当且仅当存在$S$到$u$且$v$到$T$的增广路径。

2-SAT做法：

若$u$或$v$是$o$标记，则可能不在，否则一定在。

可能有关的东西：传递闭包

先将它强连通分量缩点一下，然后图将会变成一个DAG，然后传递闭包就是一个$DP$。

就可以$dp[i]= $ 一个01串，然后转移就是$dp[i]=\bigvee\limits_{i,j\in e} dp_j$，然后可以用bitset优化。

关于这个判断：

比如第一个问题

$u$设为$S$，$v$设为$T$且不合法可以很容易推出与存在$u\to v $的增广路径等价。

如果将$u$及其能到的点设为$S$，$v$及其能到的点设为$T$，那么直接dfs是$O(n+m)$的。

但如果是判$u\to v$的增广路径的话，可以先$O(\frac{n^3}{\omega})$预处理传递闭包，然后$O(1)$判断。

原题代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

int n,m,s,t;
int head[11111],cnt_e=1,now[11111];
struct edge {int nxt,to,cap;}e[22222];
int flow[22222];
int dis[11111];
inline void add_edge(int u,int v,int c){e[++cnt_e]=(edge){head[u],v,c};head[u]=cnt_e;}
deque<int>q;
int bfs()
{
	memset(dis,0,sizeof(dis));
	q.clear();q.pb(s);
	dis[s]=1;
	int u,v;
	while((int)q.size()>0)
	{
		u=q.front();q.pop_front();
		for(int i=head[u];i;i=e[i].nxt)
		{
			v=e[i].to;
			if(dis[v]||flow[i]==e[i].cap) continue;
			dis[v]=dis[u]+1;q.pb(v);
		}
	}
	return dis[t]>0;
}
int dfs(int u,int mc)
{
	if(u==t) return mc;
	int ret=0,v,k;
	for(int i=now[u];i&&ret<mc;i=e[i].nxt)
	{
		now[u]=i;
		v=e[i].to;
		if(flow[i]==e[i].cap||dis[v]!=dis[u]+1) continue;
		k=dfs(v,min(mc-ret,e[i].cap-flow[i]));
		flow[i]+=k,flow[i^1]-=k,ret+=k;
	}
	return ret;
}
int dinic()
{
	int ret=0;
	while(bfs())
	{
		cpy(now,head,n+5);
		ret+=dfs(s,inf);
	}
	return ret;
}
int vis[111111];
int dfstag;
int dfs(int u)
{
	vis[u]=1;
	int ret=1;
	for(int _=head[u];_;_=e[_].nxt)
	{
		int i=_^dfstag,v=e[_].to;
		if(flow[i]==e[i].cap||vis[v]) continue;
		ret+=dfs(v);
	}
	return ret;
}
signed main()
{
	freopen("attack.in","r",stdin);
    freopen("attack.out","w",stdout);
	n=read(),m=read(),s=read(),t=read();
	int u,v,c;R(i,1,m) u=read(),v=read(),c=read(),add_edge(u,v,c),add_edge(v,u,c);
	dinic();
	int tmp=dfs(s);
	dfstag=1;memset(vis,0,sizeof(vis));
	tmp+=dfs(t);
	if(tmp==n) puts("UNIQUE");
	else puts("AMBIGUOUS");
}