广义后缀自动机

前置知识

广义后缀自动机基于下面的知识点

请务必对上述两个知识点非常熟悉之后，再来阅读本文，特别是对于 后缀自动机 中的 后缀链接 能够有一定的理解

起源

广义后缀自动机是由刘研绎在其 2015 国家队论文《后缀自动机在字典树上的拓展》上提出的一种结构，即将后缀自动机直接建立在字典树上。

大部分可以用后缀自动机处理的字符串的问题均可扩展到 Trie 树上。——刘研绎

约定

参考字符串约定

字符串个数为 $k$ 个，即 $S_1, S_2, S_3 … S_k$

约定字典树和广义后缀自动机的根节点为 $0$ 号节点

概述

后缀自动机 (suffix automaton, SAM) 是用于处理单个字符串的子串问题的强力工具。

而广义后缀自动机 (General Suffix Automaton) 则是将后缀自动机整合到字典树中来解决对于多个字符串的子串问题

常见的伪广义后缀自动机

通过用特殊符号将多个串直接连接后，再建立 SAM
对每个串，重复在同一个 SAM 上进行建立，每次建立前，将 last 指针置零

方法 1 和方法 2 的实现方式简单，而且在面对题目时通常可以达到和广义后缀自动机一样的正确性。所以在网络上很多人会选择此类写法，例如在后缀自动机一文中最后一个应用，便使用了方法 1

但是无论方法 1 还是方法 2，其时间复杂度较为危险

构造广义后缀自动机

根据原论文的描述，应当在多个字符串上先建立字典树，然后在字典树的基础上建立广义后缀自动机。

字典树的使用

首先应对多个串创建一棵字典树，这不是什么难事，如果你已经掌握了前置知识的前提下，可以很快的建立完毕。这里为了统一上下文的代码，给出一个可能的字典树代码。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


#define MAXN 2000000
#define CHAR_NUM 30
struct Trie {
  int next[MAXN][CHAR_NUM];  // 转移
  int tot;                   // 节点总数：[0, tot)
  void init() { tot = 1; }
  int insertTrie(int cur, int c) {
    if (next[cur][c]) return next[cur][c];
    return next[cur][c] = tot++;
  }
  void insert(const string &s) {
    int root = 0;
    for (auto ch : s) root = insertTrie(root, ch - 'a');
  }
};

这里我们得到了一棵依赖于 next 数组建立的一棵字典树。

后缀自动机的建立

如果我们把这样一棵树直接认为是一个后缀自动机，则我们可以得到如下结论

对于节点 i，其 len[i] 和它在字典树中的深度相同
如果我们对字典树进行拓扑排序，我们可以得到一串根据 len 不递减的序列。$BFS$ 的结果相同

而后缀自动机在建立的过程中，可以视为不断的插入 len 严格递增的值，且插值为 $1$。所以我们可以将对字典树进行拓扑排序后的结果做为一个队列，然后按照这个队列的顺序不断地插入到后缀自动机中。

由于在普通后缀自动机上，其前一个节点的 len 值为固定值，即为 last 节点的 len。但是在广义后缀自动机中，插入的队列是一个不严格递增的数列。所以对于每一个值，对于它的 last 应该是已知而且固定的，在字典树上，即为其父亲节点。

由于在字典树中，已经建立了一个近似的后缀自动机，所以只需要对整个字典树的结构进行一定的处理即可转化为广义后缀自动机。我们可以按照前面提出的队列顺序来对整个字典树上的每一个节点进行更新操作。最终我们可以得到广义后缀自动机。

对于每个点的更新操作，我们可以稍微修改一下 SAM 中的插入操作来得到。

对于整个插入的过程，需要注意的是，由于插入是按照 len 不递减的顺序插入，在进行 $clone$ 后的数据复制过程中，不可以复制其 len 小于当前 len 的数据。

算法

根据上述的逻辑，可以将整个构建过程描述为如下操作

将所有字符串插入到字典树中
从字典树的根节点开始进行 $BFS$，记录下顺序以及每个节点的父亲节点
将得到的 $BFS$ 序列按照顺序，对每个节点在原字典树上进行构建，注意不能将 len 小于当前 len 的数据进行操作

对操作次数为线性的证明

由于仅处理 $BFS$ 得到的序列，可以保证字典树上所有节点仅经过一次。

对于最坏情况，考虑字典树本身节点个数最多的情况，即任意两个字符串没有相同的前缀，则节点个数为 $\sum_{i=1}^{k}|S_i|$，即所有的字符串长度之和。

而在后缀自动机的更新操作的复杂度已经在后缀自动机中证明

所以可以证明其最坏复杂度为线性

而通常伪广义后缀自动机的平均复杂度等同于广义后缀自动机的最差复杂度，面对对于大量的字符串时，伪广义后缀自动机的效率远不如标准的广义后缀自动机

实现

对插入函数进行少量必要的修改即可得到所需要的函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


struct GSA {
  int len[MAXN];             // 节点长度
  int link[MAXN];            // 后缀链接，link
  int next[MAXN][CHAR_NUM];  // 转移
  int tot;                   // 节点总数：[0, tot)
  int insertSAM(int last, int c) {
    int cur = next[last][c];
    len[cur] = len[last] + 1;
    int p = link[last];
    while (p != -1) {
      if (!next[p][c])
        next[p][c] = cur;
      else
        break;
      p = link[p];
    }
    if (p == -1) {
      link[cur] = 0;
      return cur;
    }
    int q = next[p][c];
    if (len[p] + 1 == len[q]) {
      link[cur] = q;
      return cur;
    }
    int clone = tot++;
    for (int i = 0; i < CHAR_NUM; ++i)
      next[clone][i] = len[next[q][i]] != 0 ? next[q][i] : 0;
    len[clone] = len[p] + 1;
    while (p != -1 && next[p][c] == q) {
      next[p][c] = clone;
      p = link[p];
    }
    link[clone] = link[q];
    link[cur] = clone;
    link[q] = clone;
    return cur;
  }
  void build() {
    queue<pair<int, int>> q;
    for (int i = 0; i < 26; ++i)
      if (next[0][i]) q.push({i, 0});
    while (!q.empty()) {
      auto item = q.front();
      q.pop();
      auto last = insertSAM(item.second, item.first);
      for (int i = 0; i < 26; ++i)
        if (next[last][i]) q.push({i, last});
    }
  }
}

由于整个 $BFS$ 的过程得到的顺序，其父节点始终在变化，所以并不需要保存 last 指针。
插入操作中，int cur = next[last][c]; 与正常后缀自动机的 int cur = tot++; 有差异，因为我们插入的节点已经在树型结构中完成了，所以只需要直接获取即可
在 $clone$ 后的数据拷贝中，有这样的判断 next[clone][i] = len[next[q][i]] != 0 ? next[q][i] : 0; 这与正常的后缀自动机的直接赋值 next[clone][i] = next[q][i]; 有一定差异，此次是为了避免更新了 len 大于当前节点的值。由于数组中 len 当且仅当这个值被 $BFS$ 遍历并插入到后缀自动机后才会被赋值

性质

广义后缀自动机与后缀自动机的结构一致，在后缀自动机上的性质绝大部分均可在广义后缀自动机上生效（后缀自动机的性质）
当广义后缀自动机建立后，通常字典树结构将会被破坏，即通常不可以用广义后缀自动机来解决字典树问题。当然也可以选择准备双倍的空间，将后缀自动机建立在另外一个空间上。

应用

所有字符中不同子串个数

可以根据后缀自动机的性质得到，以点 $i$ 为结束节点的子串个数等于 $len[i] - len[link[i]]$

所以可以遍历所有的节点求和得到

例题：【模板】广义后缀自动机（广义 SAM）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89


#include <bits/stdc++.h>
using namespace std;
#define MAXN 2000000  // 双倍字符串长度
#define CHAR_NUM 30   // 字符集个数，注意修改下方的 (-'a')
struct exSAM {
  int len[MAXN];             // 节点长度
  int link[MAXN];            // 后缀链接，link
  int next[MAXN][CHAR_NUM];  // 转移
  int tot;                   // 节点总数：[0, tot)
  void init() {
    tot = 1;
    link[0] = -1;
  }
  int insertSAM(int last, int c) {
    int cur = next[last][c];
    if (len[cur]) return cur;
    len[cur] = len[last] + 1;
    int p = link[last];
    while (p != -1) {
      if (!next[p][c])
        next[p][c] = cur;
      else
        break;
      p = link[p];
    }
    if (p == -1) {
      link[cur] = 0;
      return cur;
    }
    int q = next[p][c];
    if (len[p] + 1 == len[q]) {
      link[cur] = q;
      return cur;
    }
    int clone = tot++;
    for (int i = 0; i < CHAR_NUM; ++i)
      next[clone][i] = len[next[q][i]] != 0 ? next[q][i] : 0;
    len[clone] = len[p] + 1;
    while (p != -1 && next[p][c] == q) {
      next[p][c] = clone;
      p = link[p];
    }
    link[clone] = link[q];
    link[cur] = clone;
    link[q] = clone;
    return cur;
  }
  int insertTrie(int cur, int c) {
    if (next[cur][c]) return next[cur][c];
    return next[cur][c] = tot++;
  }
  void insert(const string &s) {
    int root = 0;
    for (auto ch : s) root = insertTrie(root, ch - 'a');
  }
  void insert(const char *s, int n) {
    int root = 0;
    for (int i = 0; i < n; ++i) root = insertTrie(root, s[i] - 'a');
  }
  void build() {
    queue<pair<int, int>> q;
    for (int i = 0; i < 26; ++i)
      if (next[0][i]) q.push({i, 0});
    while (!q.empty()) {
      auto item = q.front();
      q.pop();
      auto last = insertSAM(item.second, item.first);
      for (int i = 0; i < 26; ++i)
        if (next[last][i]) q.push({i, last});
    }
  }
} exSam;
char s[1000100];
int main() {
  int n;
  cin >> n;
  exSam.init();
  for (int i = 0; i < n; ++i) {
    cin >> s;
    int len = strlen(s);
    exSam.insert(s, len);
  }
  exSam.build();
  long long ans = 0;
  for (int i = 1; i < exSam.tot; ++i) {
    ans += exSam.len[i] - exSam.len[exSam.link[i]];
  }
  cout << ans << endl;
}

多个字符串间的最长公共子串

我们需要对每个节点建立一个长度为 $k$ 的数组 flag（对于本题而言，可以仅为标记数组，若需要求出此子串的个数，则需要改成计数数组）

在字典树插入字符串时，对所有节点进行计数，保存在当前字符串所在的数组

然后按照 len 递减的顺序遍历，通过后缀链接将当前节点的 flag 与其他节点的合并

遍历所有的节点，找到一个 len 最大且满足对于所有的 k，其 flag 的值均为非 $0$ 的节点，此节点的 $len$ 即为解

例题：SPOJ Longest Common Substring II

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127


#include <bits/stdc++.h>
using namespace std;
#define MAXN 2000000  // 双倍字符串长度
#define CHAR_NUM 30   // 字符集个数，注意修改下方的 (-'a')
#define NUM 15        // 字符串个数
struct exSAM {
  int len[MAXN];             // 节点长度
  int link[MAXN];            // 后缀链接，link
  int next[MAXN][CHAR_NUM];  // 转移
  int tot;                   // 节点总数：[0, tot)
  int lenSorted[MAXN];   // 按照 len 排序后的数组，仅排序 [1, tot)
                         // 部分，最终下标范围 [0, tot - 1)
  int sizeC[MAXN][NUM];  // 表示某个字符串的子串个数
  int curString;         // 字符串实际个数
  /**
   * 计数排序使用的辅助空间数组
   */
  int lc[MAXN];  // 统计个数
  void init() {
    tot = 1;
    link[0] = -1;
  }
  int insertSAM(int last, int c) {
    int cur = next[last][c];
    len[cur] = len[last] + 1;
    int p = link[last];
    while (p != -1) {
      if (!next[p][c])
        next[p][c] = cur;
      else
        break;
      p = link[p];
    }
    if (p == -1) {
      link[cur] = 0;
      return cur;
    }
    int q = next[p][c];
    if (len[p] + 1 == len[q]) {
      link[cur] = q;
      return cur;
    }
    int clone = tot++;
    for (int i = 0; i < CHAR_NUM; ++i)
      next[clone][i] = len[next[q][i]] != 0 ? next[q][i] : 0;
    len[clone] = len[p] + 1;
    while (p != -1 && next[p][c] == q) {
      next[p][c] = clone;
      p = link[p];
    }
    link[clone] = link[q];
    link[cur] = clone;
    link[q] = clone;
    return cur;
  }
  int insertTrie(int cur, int c) {
    if (!next[cur][c]) next[cur][c] = tot++;
    sizeC[next[cur][c]][curString]++;
    return next[cur][c];
  }
  void insert(const string &s) {
    int root = 0;
    for (auto ch : s) root = insertTrie(root, ch - 'a');
    curString++;
  }
  void insert(const char *s, int n) {
    int root = 0;
    for (int i = 0; i < n; ++i) root = insertTrie(root, s[i] - 'a');
    curString++;
  }
  void build() {
    queue<pair<int, int>> q;
    for (int i = 0; i < 26; ++i)
      if (next[0][i]) q.push({i, 0});
    while (!q.empty()) {
      auto item = q.front();
      q.pop();
      auto last = insertSAM(item.second, item.first);
      for (int i = 0; i < 26; ++i)
        if (next[last][i]) q.push({i, last});
    }
  }
  void sortLen() {
    for (int i = 1; i < tot; ++i) lc[i] = 0;
    for (int i = 1; i < tot; ++i) lc[len[i]]++;
    for (int i = 2; i < tot; ++i) lc[i] += lc[i - 1];
    for (int i = 1; i < tot; ++i) lenSorted[--lc[len[i]]] = i;
  }
  void getSizeLen() {
    for (int i = tot - 2; i >= 0; --i)
      for (int j = 0; j < curString; ++j)
        sizeC[link[lenSorted[i]]][j] += sizeC[lenSorted[i]][j];
  }
  void debug() {
    cout << "     i      len      link       ";
    for (int i = 0; i < 26; ++i) cout << "  " << (char)('a' + i);
    cout << endl;
    for (int i = 0; i < tot; ++i) {
      cout << "i: " << setw(3) << i << " len: " << setw(3) << len[i]
           << " link: " << setw(3) << link[i] << " Next: ";
      for (int j = 0; j < CHAR_NUM; ++j) {
        cout << setw(3) << next[i][j];
      }
      cout << endl;
    }
  }
} exSam;
int main() {
  exSam.init();
  string s;
  while (cin >> s) exSam.insert(s);
  exSam.build();
  exSam.sortLen();
  exSam.getSizeLen();
  int ans = 0;
  for (int i = 0; i < exSam.tot; ++i) {
    bool flag = true;
    for (int j = 0; j < exSam.curString; ++j) {
      if (!exSam.sizeC[i][j]) {
        flag = false;
        break;
      }
    }
    if (flag) ans = max(ans, exSam.len[i]);
  }
  cout << ans << endl;
}

以上搬运自oi-wiki

然而oi-wiki上讲的是离线做法。为将多个模式串离线插入到$\text{Trie}$树中，然后依据$\text{Trie}$构造广义SAM.

而还有一种在线构造的做法，指不建立$\text{Trie}$，直接把给出的多个模式串依次插入到广义SAM中。下面开始搬辰星凌神仙的博客

具体来说，每次插入一个模式串之前，都把$last$设为$1$，$insert$函数在普通SAM的基础上加入特判（注意前面说的盗版写法用的是不加特判的普通$insert$）。

更新后的代码大概如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


struct exSAM
{
	int tn;
	struct node {int len,nxt,son[26];}a[N<<1];
	inline void init_SAM() {tn=1;}
	inline int extend_SAM(int lst,int c)//将ch[now]接到last后面
	{
		if(a[lst].son[c]&&a[lst].len+1==a[a[lst].son[c]].len) return a[lst].son[c];//特判1
		int cur=++tn,p=lst,flag=0,v,x;
		for(;p&&!a[p].son[c];p=a[p].nxt)a[p].son[c]=cur;
		if(!p) a[cur].nxt=1;
		else
		{
			v=a[p].son[c];
			if(a[v].len==a[p].len+1) a[cur].nxt=v;
			else
			{
				if(a[cur].len==a[p].len+1/*or p==lst*/)flag=1;//特判2
				x=++tn;a[x]=a[v];a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[cur].nxt=a[v].nxt=x;
			}
		} 	
		return flag?x:cur;
		//返回值为:ch[now]插入到SAM中的节点编号，
    	//如果now不是某个字符串的最后一个字符,
    	//那么这次返回值将作为下一次插入时的last
	}
};

稍微解释一下两个特判。

特判1：在$lst$后插入一个节点$cur$满足$maxlen[cur]=maxlen[lst]+1$，而如果这个节点已经在SAM中了，那么就可以直接返回。

注意，这里返回的这个节点保存了多个模式串的状态，即将多个不同模式串的相同子串信息压缩在了这一个节点内，如果要记录${endpos}$大小的话，则需要给每个模式串都单独维护一个$siz$数组依次更新，而不能全部揉成一团

特判2的实质是处理$a[lst].son[i]\ne NULL$且$maxlen[lst]+1\ne maxlen[a[lst].son[i]]$的情况。

单串SAM的$insert$图示

图源：hihocoder

在从$last$开始往前跳parent树时，单串SAM必定存在$a[p].son[c]=NULL$的一段（在图中表现为以$u$节点结尾的最右边那一段），但扩展到多串后可能就没有这一段了，即存在$a[lst].son[i]=cur$且$maxlen[lst]+1\ne maxlen[x]$（若$maxlen[lst]+1=maxlen[cur]$的情况在特判1时就返回了）。

显然，此时没有任何节点的转移函数son或parent指针（后缀链接）指向最初新建cur的节点，同时它没有记录任何信息，因为新加入的信息全部存储在了$a[cur].nxt=x$节点上面，即从v拆出来的那个点 ，即cur是一个空节点。

可以用$minlen,maxlen$的大小推导出$cur$为空：

$cur$的parent指针会指向$v$的拆分节点$x$，而$maxlen[x]=maxlen[lst]+1$，所以$minlen[cur]=maxlen[a[cur].nxt=x]+1=maxlen[lst]+2$，又有$maxlen[cur]=maxlen[lst]+1<minlen[cur]$，而一个等价类维护的子串长度$\in[minlen,maxlen]$故$cur$为空。

从另一个角度看，节点$x$满足$a[lst].son[c]=x$且$maxlen[x]=maxlen[lst]+1$，这不正是我们需要的吗（同特判1）。所以可以返回$x$，并使用$x$作为当前模式串下一次$insert$的$lst$。

还剩下最后一个问题：前面说的这两个特判能正确地合并好等价类，但没有处理空节点$cur$。为使构造出自动机节点数与离线做法一致，我们还需进一步改进：当存在$a[lst].son[c]$时就新建$cur$节点了，直接从拆分节点开始做（或者在拆分节点之前通过特判1返回）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


const int N=2e6+10;
char str[N];
int s[N];
int n;

struct exSAM
{
	int tn;
	struct node {int len,nxt,son[26];}a[N<<1];
	inline void init_SAM() {tn=1;}
	inline int extend_SAM(int lst,int c)//将ch[now]接到last后面
	{
		if(a[lst].son[c])
		{
			int p=lst,v=a[p].son[c];
			if(a[p].len+1==a[v].len)return v;//最初的特判1
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[v].nxt=x;
				return x;//即最初的特判2	
			}
		}
		int cur=++tn,p=lst;
		a[cur].len=a[p].len+1;
		for(;p&&!a[p].son[c];p=a[p].nxt)a[p].son[c]=cur;
		if(!p) a[cur].nxt=1;
		else
		{
			int v=a[p].son[c];
			if(a[v].len==a[p].len+1)a[cur].nxt=v;
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[cur].nxt=a[v].nxt=x;
			}
		}
		return cur;
	}
	inline void instr(char *s){int p=1;for(;*s;s++){p=extend_SAM(p,*s-'a');}}
	inline void solve() {int ans=0;R(i,2,tn)ans+=a[i].len-a[a[i].nxt].len;writeln(ans);}
}sm;
signed main()
{
	n=read();
	sm.init_SAM();
	R(i,1,n) scanf("%s",str),sm.instr(str);
	sm.solve();
}

这里补充两张图，模拟最终版代码构造过程中特判2的运作（根为1，转移函数$trans$为黑边，后缀链接$link$为灰边）：

（图一：串$aab$构造结束后的形态）

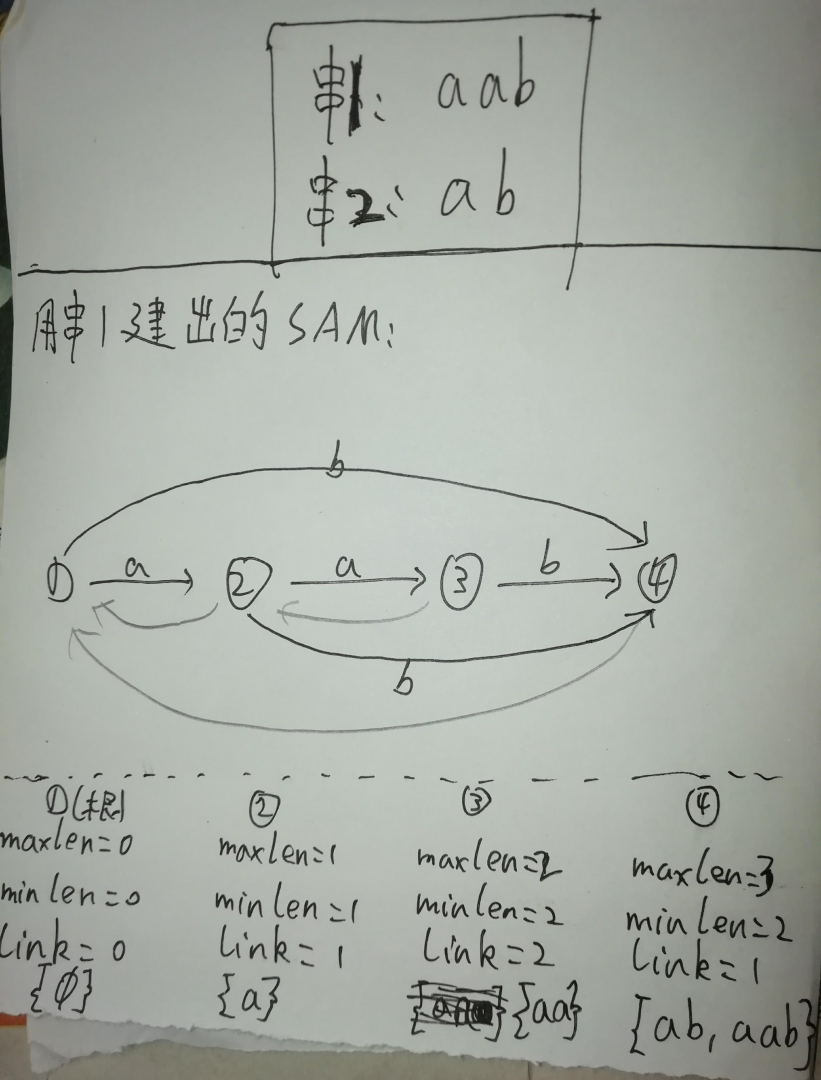
（图2：插入串$ab$中第二个字符$b$时的形态变换过程）

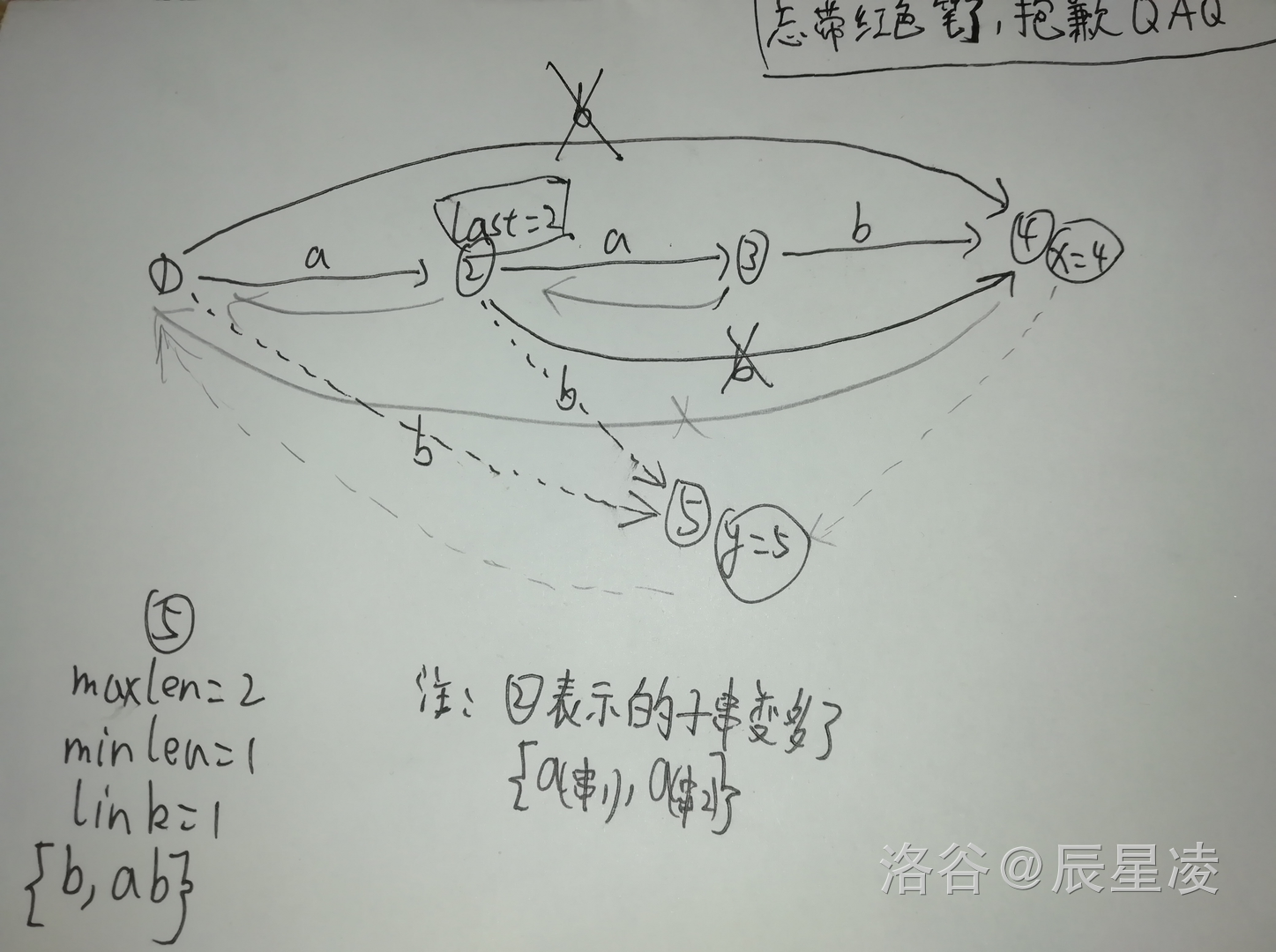
如上方黑体字所说，此时一个节点可能会存储多个字符串的信息，比如节点2：虽然表示的子串都为${a}$，但${endpos}$大小却不相同（$siz_{aab}(2)=2,siz_{ab}(2)=1$）。

在线和离线的不同：在特判的作用下，在线写法会构造出一颗类$\text{Trie}$形态的SAM，其本质还是在一颗没有具象化的$\text{Trie}$树上建立了SAM。

分别维护不同串的siz

例题:[HAOI2016]找相同字符

题意：求两个字符串的相同子串数量。

两个串的$|endpos|$需要分开来计算，可以开一个二维数组，用$six[x][id]$表示节点$x$在串$id$上的${endpos}$大小。

则答案为： $$ \sum siz_{i,0}\times siz_{i,1}\times(len[i]-len[link[i]]) $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80


const int N=8e5+10;
char str[N];
int in[N];

struct exSAM
{
	vector<int>e[N];

	int tn,ans;
	struct node {int len,nxt,son[26];}a[N];
	int siz[N][2];
	inline void init_SAM() {tn=1;ans=0;}
	inline int extend_SAM(int lst,int c,int id)//将ch[now]接到last后面
	{
		if(a[lst].son[c])
		{
			int p=lst,v=a[p].son[c];
			if(a[p].len+1==a[v].len){siz[v][id]=1;return v;}
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[v].nxt=x;
				siz[x][id]=1;
				return x;//即最初的特判2	
			}
		}
		int cur=++tn,p=lst;
		a[cur].len=a[p].len+1;
		for(;p&&!a[p].son[c];p=a[p].nxt)a[p].son[c]=cur;
		if(!p) a[cur].nxt=1;
		else
		{
			int v=a[p].son[c];
			if(a[v].len==a[p].len+1)a[cur].nxt=v;
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[cur].nxt=a[v].nxt=x;
			}
		}
		siz[cur][id]=1;
		return cur;
	}
	inline void instr(char *s,int id){int p=1;for(;*s;s++){p=extend_SAM(p,*s-'a',id);}}
	inline void dfs(int u){for(int v:e[u]) dfs(v),siz[u][0]+=siz[v][0],siz[u][1]+=siz[v][1];}
	inline void solve()
	{
		R(i,2,tn) e[a[i].nxt].pb(i);
		dfs(1);
		/*
		deque<int>q;
		R(i,2,tn) ++in[a[i].nxt];
		R(i,1,tn) if(!in[i]) q.pb(i);
		while((int)q.size()>0)
		{
			int u=q.front();q.pop_front();
			siz[a[u].nxt][0]+=siz[u][0];
			siz[a[u].nxt][1]+=siz[u][1];
			if(!(--in[a[u].nxt])) q.pb(a[u].nxt);
		}
		*/		
		//R(i,2,tn) printf("%lld %lld %lld %lld %lld %lld\n",i,a[i].nxt,siz[i][0],siz[i][1],a[i].len,a[a[i].nxt].len);
		R(i,2,tn) ans+=1ll*siz[i][0]*siz[i][1]*(a[i].len-a[a[i].nxt].len); 
		writeln(ans);
	}	
}sm;
signed main()
{
	sm.init_SAM();
	R(i,0,1) 
	{
		scanf("%s",str);
		sm.instr(str,i);
	}
	sm.solve();
}

线段树合并维护siz

CF666E Forensic Examination

给定一个串$S$以及$m$个$T_i$串，有$q$次询问，每次询问$S$的子串$S[p_l\dots p_r]$在$T_{l\dots r}$中的哪个串里的出现次数最大，并输出出现次数。如果有多解输出最靠前的那一个。

先把所有字符串都插入到广义SAM中，对于每个节点开一棵下标为$[1,m]$的线段树（动态开点）线段树维护$siz$（注意插入$S$就不要在线段树上进行修改操作了）。由于$siz$的维护是统计子树和，所以插入结束后要在$parent$树上跑一下线段树合并。

查询时先在$parent$树上倍增找到包含子串$S[p_l,p_r]$的等价类状态节点，然后在该点的线段树上查询区间$[l,r]$中的最大值，顺便维护下最大值所处位置即可。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191


#include<bits/stdc++.h>
#define ld long double
#define tset puts("qwq");
#define test puts("QAQ");
#define pb(a) push_back(a)
#define pii pair<int,int> 
#define mkp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
//#define int long long
#define R(i,a,b) for(int i=(a),i##E=(b);i<=i##E;i++)
#define L(i,a,b) for(int i=(b),i##E=(a);i>=i##E;i--)
#define clr(f,n) memset(f,0,sizeof(int)*(n))
#define cpy(f,g,n) memcpy(f,g,sizeof(int)*(n))
#define Swap(x,y) (x^=y^=x^=y)
template <typename T> bool ckmax(T &x, T y) { return x<y?x=y,true:false;}
template <typename T> bool ckmin(T &x, T y) { return x>y?x=y,true:false;}
using namespace std;
//const ll inf=0x7f7f7f7f7f7f7f3f;
const ll inf=(1ll<<60);
//const int inf=0x7f7f7f7f;
//const int mod=1e9+7;
const double Pi=acos(-1);
const int mod=1e9+7;
const double eps=1e-6;
inline int fpow(int a,int b=mod-2,int p=mod){int res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;}
/*
const int qwq=8000010;
int F[qwq],inv[qwq],Finv[qwq];
void init_C()
{
    F[0]=Finv[0]=inv[1]=1;
    R(i,2,qwq-10) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    R(i,1,qwq-10) F[i]=1ll*(F[i-1]*i)%mod,Finv[i]=1ll*(Finv[i-1]*inv[i])%mod;
}

inline int C(int n,int m){ if(m<0||m>n||n<0) return 0;return 1ll*F[n]%mod*1ll*Finv[m]*1ll%mod*1ll*Finv[n-m]%mod;}
*/

//#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
inline ll read()
{
    char c=getchar();ll x=0;bool f=0;
    for(;!isdigit(c);c=getchar())f^=!(c^45);
    for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
    if(f)x=-x;
    return x;
}
inline void write(ll x){if (x<0){putchar('-');write(-x);return;}if (x>=10) write(x/10);putchar(x%10+'0');}
inline void writesp(ll x){write(x),putchar(' ');}
inline void writeln(ll x){write(x);putchar('\n');}
/*
unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
mt19937 rand_num(seed);  
uniform_int_distribution<long long> dist(0, 10000000);  // ¸ø¶¨·¶Î§
printf("%lld ",dist(rand_num));
*/
const int N=2e6+10;
int n,m;
char strs[N],strt[N];
int pos[N];

struct node {
	int val,pos;
	inline int operator <(const node &A)const {return (val^A.val)?val<A.val:pos>A.pos;}
};	
inline node MAX(const node &A,const node &B) {return A<B?B:A;}
int Rt[N];

namespace st
{
	int tot_seg;
	int Ls[N<<1],Rs[N<<1];
	node tr[N<<1];
	inline void push_up(int x) {tr[x]=MAX(tr[Ls[x]],tr[Rs[x]]);}
	void modify(int pos,int l,int r,int &x)
	{
		if(!x) x=++tot_seg;
		if(l==r) {++tr[x].val,tr[x].pos=l;return;}
		int mid=(l+r)>>1;
		if(pos<=mid) modify(pos,l,mid,Ls[x]);
		else modify(pos,mid+1,r,Rs[x]);
		push_up(x);
	}	
	int mer(int l,int r,int x,int y)
	{
		if(!x||!y) return x^y;
		int cur=++tot_seg;
		if(l==r) {tr[cur]=tr[x],Ls[cur]=Ls[x],Rs[cur]=Rs[x],tr[cur].val+=tr[y].val;return cur;}
		int mid=(l+r)>>1;
		Ls[cur]=mer(l,mid,Ls[x],Ls[y]);
		Rs[cur]=mer(mid+1,r,Rs[x],Rs[y]);
		push_up(cur);
		return cur;
	}
	node query(int L,int R,int l,int r,int x)
	{
		if(!x) return (node){0,m+1};
		if(L<=l&&r<=R) return tr[x];
		node ret;ret.val=0,ret.pos=m+1;
		int mid=(l+r)>>1;
		if(L<=mid) ret=MAX(ret,query(L,R,l,mid,Ls[x]));
		if(mid<R) ret=MAX(ret,query(L,R,mid+1,r,Rs[x]));
		return ret;
	}
}
namespace sm
{
	vector<int>e[N];
	int dep[N],fa[23][N];
	int tn;
	struct node {int len,nxt,son[26];}a[N];
	inline void init_SAM() {tn=1;}
	inline int extend_SAM(int lst,int c,int id)
	{
		if(a[lst].son[c]) 
		{
			int p=lst,v=a[p].son[c];
			if(a[p].len+1==a[v].len){if(id)st::modify(id,1,m,Rt[v]);return v;}
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[v].nxt=x;
				if(id) st::modify(id,1,m,Rt[x]);
				return x;
			}
		}
		int cur=++tn,p=lst;
		a[cur].len=a[p].len+1;
		for(;p&&!a[p].son[c];p=a[p].nxt)a[p].son[c]=cur;
		if(!p) a[cur].nxt=1;
		else
		{
			int v=a[p].son[c];
			if(a[v].len==a[p].len+1)a[cur].nxt=v;
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[cur].nxt=a[v].nxt=x;
			}
		}
		if(id) st::modify(id,1,m,Rt[cur]);
		return cur;
	}
	inline void instrt(char *s,int id){int p=1;for(;*s;s++){p=extend_SAM(p,*s-'a',id);}}
	inline void instrs(char *s){int p=1;for(int i=0;s[i];i++)pos[i+1]=p=extend_SAM(p,s[i]-'a',0);}
	void dfs1(int u,int f)
	{
		dep[u]=dep[f]+1;
		fa[0][u]=f;
		for(int i=1;(1<<i)<=dep[u];i++)fa[i][u]=fa[i-1][fa[i-1][u]];
		for(int v:e[u]) dfs1(v,u),Rt[u]=st::mer(1,m,Rt[u],Rt[v]);
	}
	inline void build() 
	{
		R(i,2,tn) e[a[i].nxt].pb(i);
		dfs1(1,0);
	}
	inline int find_fa(int u,int len) 
	{
		int p=pos[u];
		L(i,0,21) if(fa[i][p]&&a[fa[i][p]].len>=len) p=fa[i][p];
		return p;
	}
	inline void solve(int l,int r,int x,int y)
	{
		auto ans=st::query(l,r,1,m,Rt[find_fa(y,y-x+1)]);
		if(!ans.val) ans.pos=l;
		printf("%d %d\n",ans.pos,ans.val);
	}
} 
signed main()
{
	sm::init_SAM();
	scanf("%s",strs);
	n=strlen(strs);
	m=read();
	R(i,1,m) scanf("%s",strt),sm::instrt(strt,i);
	sm::instrs(strs);
	//R(i,0,10) printf("%lld\n",pos[i]);
	sm::build();
	int l,r,x,y;
	for(int _=read();_;_--) l=read(),r=read(),x=read(),y=read(),sm::solve(l,r,x,y);
}

树上本质不同的路径数

P3346 [ZJOI2015]诸神眷顾的幻想乡

题意：

给出一棵叶子节点不超过20个的无根树，每个节点上都有一个不超过10的数字，求树上本质不同的路径数（两条路径相同定义为：其路径上所有节点上的数字依次相连组成的字符串相同）。

首先有一个很麻烦的地方在于路径可以是在lca两个不同儿子节点的子树中。

而Trie树和各种自动机在"接受"字符串时都是以根为起点从上往下径直走到底。

所以要想办法把路径弄直，这里有一个不太容易想出来的的结论：

一颗无根树上任意一条路径必定可以在以某个叶节点为根时，变成一条从上到下的路径（利于广义SAM的使用）。

而题面说叶子节点不超过20个。

意味我们可以暴力枚举每一个叶节点作为根节点遍历整棵树。

将$tot_{leaf}$棵树中的所有前缀串都抽出来建立广义SAM，然后直接求本质不同的子串的个数。

这里的前缀串的定义为从根节点（无根树的某个叶子节点）到任意一个节点的路径所构造成的字符串。（其实就是$tot_{leaf}$棵Trie树合在一起跑广义SAM）。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124


#include<bits/stdc++.h>
#define ld long double
#define tset puts("qwq");
#define test puts("QAQ");
#define pb(a) push_back(a)
#define pii pair<int,int> 
#define mkp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define int long long
#define R(i,a,b) for(int i=(a),i##E=(b);i<=i##E;i++)
#define L(i,a,b) for(int i=(b),i##E=(a);i>=i##E;i--)
#define clr(f,n) memset(f,0,sizeof(int)*(n))
#define cpy(f,g,n) memcpy(f,g,sizeof(int)*(n))
#define Swap(x,y) (x^=y^=x^=y)
template <typename T> bool ckmax(T &x, T y) { return x<y?x=y,true:false;}
template <typename T> bool ckmin(T &x, T y) { return x>y?x=y,true:false;}
using namespace std;
//const ll inf=0x7f7f7f7f7f7f7f3f;
const ll inf=(1ll<<60);
//const int inf=0x7f7f7f7f;
//const int mod=1e9+7;
const double Pi=acos(-1);
const int mod=1e9+7;
const double eps=1e-6;
inline int fpow(int a,int b=mod-2,int p=mod){int res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;}
/*
const int qwq=8000010;
int F[qwq],inv[qwq],Finv[qwq];
void init_C()
{
    F[0]=Finv[0]=inv[1]=1;
    R(i,2,qwq-10) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    R(i,1,qwq-10) F[i]=1ll*(F[i-1]*i)%mod,Finv[i]=1ll*(Finv[i-1]*inv[i])%mod;
}

inline int C(int n,int m){ if(m<0||m>n||n<0) return 0;return 1ll*F[n]%mod*1ll*Finv[m]*1ll%mod*1ll*Finv[n-m]%mod;}
*/

//#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
inline ll read()
{
    char c=getchar();ll x=0;bool f=0;
    for(;!isdigit(c);c=getchar())f^=!(c^45);
    for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
    if(f)x=-x;
    return x;
}
inline void write(ll x){if (x<0){putchar('-');write(-x);return;}if (x>=10) write(x/10);putchar(x%10+'0');}
inline void writesp(ll x){write(x),putchar(' ');}
inline void writeln(ll x){write(x);putchar('\n');}
/*
unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
mt19937 rand_num(seed);  
uniform_int_distribution<long long> dist(0, 10000000);  // ¸ø¶¨·¶Î§
printf("%lld ",dist(rand_num));
*/
const int N=4e6+10;
int n,C;
int a[N];

vector<int>e[N];
namespace sm
{
	int tn;
	struct node {int len,nxt,son[10];}a[N];
	inline void init_SAM() {tn=1;}
	inline int extend_SAM(int lst,int c)
	{
		if(a[lst].son[c])
		{
			int p=lst,v=a[p].son[c];
			if(a[p].len+1==a[v].len) return v;
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[v].nxt=x;
				return x;
			}
		}
		int cur=++tn,p=lst;
		a[cur].len=a[p].len+1;
		for(;p&&!a[p].son[c];p=a[p].nxt)a[p].son[c]=cur;
		if(!p) a[cur].nxt=1;
		else
		{
			int v=a[p].son[c];
			if(a[v].len==a[p].len+1)a[cur].nxt=v;
			else
			{
				int x=++tn;a[x]=a[v];
				a[x].len=a[p].len+1;
				for(;p&&a[p].son[c]==v;p=a[p].nxt)a[p].son[c]=x;
				a[cur].nxt=a[v].nxt=x;
			}
		}
		return cur;
	}
	inline void solve() 
	{
		int ans=0;
		R(i,2,tn) ans+=a[i].len-a[a[i].nxt].len;
		writeln(ans);
	}	
}
void dfs(int u,int f,int fpos)
{
	int upos=sm::extend_SAM(fpos,a[u]);
	for(int v:e[u]) if(v^f) dfs(v,u,upos);
}
signed main()
{
	sm::init_SAM();
	n=read(),C=read();
	R(i,1,n) a[i]=read();
	int u,v;R(i,2,n)u=read(),v=read(),e[u].pb(v),e[v].pb(u);
	R(i,1,n) if(e[i].size()==1) dfs(i,0,1);
	sm::solve();
}

还需要做的:例题 : SP8093 JZPGYZ - Sevenk Love Oimaster

cmd博客广义SAM部分

但是我先鸽了qwq

文章目录