本文章仅为菜鸡给自己参考,文章特别乱
nonononononononononononono
oi-wiki
自为风月马前卒
鏡音リン
诱导排序与 SA-IS 算法
[2004]后缀数组 by. 徐智磊
[2009]后缀数组——处理字符串的有力工具 by. 罗穗骞
Flying2018字符串算法学习笔记
Flying2018-SA-IS学习笔记
blackfrog
ctz’s blog
倍增+$sort$,$O(n\log ^2n)$做法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
const int N=1e6+10;
char s[N];
int n,lim;
int sa[N],rk[N<<1],ork[N<<1];
signed main()
{
scanf("%s",s+1);
n=strlen(s+1);
R(i,1,n) sa[i]=i,rk[i]=s[i];
for(lim=1;lim<n;lim<<=1)
{
sort(sa+1,sa+n+1,[&](int x,int y){return rk[x]==rk[y]?rk[x+lim]<rk[y+lim]:rk[x]<rk[y];});
cpy(ork,rk,n<<1);
//memcpy(ork,rk,sizeof(rk));
int cnt=0;
R(i,1,n)
{
if(ork[sa[i]]==ork[sa[i-1]]&&ork[sa[i]+lim]==ork[sa[i-1]+lim]) rk[sa[i]]=cnt;
else rk[sa[i]]=++cnt;
}
}
R(i,1,n) writesp(sa[i]);
}
|
倍增+基数排序$O(n\log n)$求法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
const int N=1e6+10;
#define cmp(x,y,w) (ornk[x]==ornk[y]&&ornk[x+w]==ornk[y+w])
void get_SA(char *s,int *sa,int *rnk,int n)
{
static int m,cnt[N],osa[N],ornk[N<<1],px[N];m=0;
R(i,1,n) ++cnt[(int)s[i]],ckmax(m,(int)s[i]);
R(i,2,m) cnt[i]+=cnt[i-1];
L(i,1,n) sa[cnt[(int)s[i]]--]=i;
m=0;R(i,1,n) rnk[sa[i]]=s[sa[i]]==s[sa[i-1]]?m:++m;
for(int lim=1;m<n;lim<<=1)
{
clr(cnt,m+5),cpy(ornk+1,rnk+1,n+1);
R(i,n-lim+1,n) osa[++cnt[0]]=i;
//L(i,n-lim+1,n) osa[++cnt[0]]=i;
R(i,1,n) if(sa[i]>lim) osa[++cnt[0]]=sa[i]-lim;
//R(i,1,n) ++cnt[rnk[i]];
R(i,1,n) ++cnt[px[i]=rnk[osa[i]]];
R(i,2,m) cnt[i]+=cnt[i-1];
//L(i,1,n) sa[cnt[rnk[osa[i]]]--]=osa[i];
L(i,1,n) sa[cnt[px[i]]--]=osa[i];
m=0;R(i,1,n) rnk[sa[i]]=cmp(sa[i],sa[i-1],lim)?m:++m;
if(m==n) {R(i,1,n)sa[rnk[i]]=i;break;}
}
}
int n,sa[N],rnk[N];
char s[N];
signed main()
{
scanf("%s",s+1);
n=strlen(s+1);
get_SA(s,sa,rnk,n);
R(i,1,n) writesp(sa[i]);
}
|
下面为两个$O(n)$做法
诱导排序与 SA-IS 算法:
SA-IS全称Suffix Array Induce Sort,即诱导后缀排序。
为了方便,我们在末尾加上一个特殊字符#。我们认为特殊字符字典序最小。
用$rk_i$表示后缀$i$的排名,$sa_i$表示排名为$i$的后缀,有$sa_{rk_i}=i$。
定义:如果一段后缀$i$有$rk_i>rk_{i+1}$那么$i$为$L$型后缀,否则$i$为$S$型后缀。
不妨设$tp_i=[i$是$L$型后缀$]$。特别的,特殊字符是$S$型后缀。
关于字典序的一个性质:
引理1.1 $A<B$当且仅当$A[lcp(A,B)]<B[lcp(A,B)]$。
证明 这个结论显然成立,因为$prefix(A,lcp(A,B)-1)=prefix(B,lcp(A,B)-1)$。
2. 1后缀类型
根据字符串的比较,其实我们可以很容易的得出一个后缀是$L$型还是$S$型。具体来说,如果$s_i=s_{i+1}$则$tp_i=tp_{i+1}$否则$tp_i=[s_i>s_{i+1}]$
(这里懒得打了直接贴别人的了qwq

2.2 LMS子串
我们求出这个$tp$之后能推出什么呢?考虑一字符串,它一定是由若干个$SS\cdots SLL\cdots LSS \cdots$构成的。
因此我们在后缀类型的$S$型中挑出特别的一类,记为$$型。$$型是$S$型的一种,它的特殊之处在于它要求它在左边的后缀必须是$L$型的。(可以将其理解为一连串$S$型中最靠左的一个。LMS(LeftMost S-type)便是这个意思)。
同时注意到,后缀#始终是$$型的。对于每一个$$型所对应上的字符,我们称为LMS字符。
而我们将位置相邻的两个LMS字符中间(包括这两个字符)所构成的子串称为LMS子串。特殊的,最后一个字符#单独作为一个平凡的LMS子串。
1
2
3
4
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
s[i]: m m i i s s i i s s i i p p i i #
tp[i]:L L S S L L S S L L S S L L L L S
* * * *
|
在上面的实例中,下标为$3,7,11,17$都是LMS字符。
而$[3,7],[7,11],[11,17],[17,17]$都是LMS子串。注意这里区间都是闭区间,也就是相邻的LMS子串有$1$的相交。

- 后面我们将会有更好的算法来对 LMS 子串排序,时间复杂度一致,但在实际运用中速度快很多。
- 注意之后会创建新字符串$S1$,其字符集$\sum$ 是不同的。
- 判断两个 LMS 子串是否相等可以暴力判断,基于引理 2.6,可以证明其总复杂度为$O(|S|)$。
1
2
3
4
5
6
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
s[i]: m m i i s s i i s s i i p p i i #
tp[i]:L L S S L L S S L L S S L L L L S
* * * *
新名称 2 2 1 0
S1: 2 2 1 0
|

2.3从SA1诱导至SA
从上面的引理2.8得知,只有获得了$S_1$的后缀数组$SA_1$,就可以得到所有$$型后缀的相对顺序。如果我们可以利用$$型后缀的相对顺序来对其他的$L$型和$S$型后缀(注意$*$型后缀也属于$S$型后缀,因此会对它们进行重排,从而确保新加入的$S$型后缀的顺序是对的。)进行排序,就可以完成后缀数组的计算。
在这里我们先假定$SA_1$已经计算出来,只需考虑如何计算$SA$。在这之前,我们先观察一下后缀数组的形式。以$aabaaaab$为例,它的后缀数组是这样的:
1
2
3
4
5
6
7
8
9
|
#
aaaab#
aaab#
aab#
aabaaaab#
ab#
abaaaab#
b#
baaaab#
|
不难发现,首字母相同的后缀是连续排布的,这一点可以用反证法来证明。因此我们可以利用桶排序的思想,为每一个出现过的字符建一个桶,用$SA$数组来存储这些桶,每个桶之间按照字典序排列,这样就可以让后缀数组初步有序。我们对每个后缀都赋予一个后缀类型,那么在首字母一样的情况下,那么在首字母一样的情况下,$S$型或$L$型会连续分布吗?答案是肯定的。因为根据引理2.2,首字母相同的后缀如果后缀类型不同,则相对顺序是确定的。因此易知不会出现$S$型和$L$型交替出现的情况。更进一步,由于$L$型后缀更小,因此总是先排布$L$型后缀,再排布$S$型后缀。因此每一个字符的桶可以分为两部分,一个用于放置$L$型后缀,另一个则用于$S$型后缀。为了方便确定每一个桶的起始位置,$S$型后缀的桶放置是倒序的。但是如果首字母和后缀类型都一致,我们不能直接快速判断大小关系。在这里就要利用诱导排序。
诱导排序的过程分为以下几步:
- 将$SA$数组初始化为每个元素都为$-1$的数组。
- 确定每个桶$S$型桶的起始位置。将$SA_1$中的每一个$*$型后缀按照$SA_1$中的顺序放入相应的桶内。
- 确定每个桶$L$型桶的起始位置。在$SA$数组中从左往右扫一遍。如果$SA_i>0$且$tp[SA_i-1]=L$,则将$SA_i-1$代表的后缀防区对应的桶中。
- 重新确定每个桶$S$型桶的起始位置,因为所有的$*$型后缀要重新被排序。由于$S$型桶是逆序排放的,所以这次从右至左地扫描一遍$SA$。如果$SA_i>0$且$tp[SA_i-1]=S$,则将$SA_i-1$所代表的后缀放入对应的桶中。
这样我们就可以完成从$SA_1$诱导到$SA$的排序工作。这里简单说明一下为什么这样做是正确的:首先对于所有的$$型后缀,都是有序排放的。从左至右扫描$SA$数组实际上就是按照字典序扫描现有的已排序的后缀。对于两个相邻的$L$型后缀$A$和$B$,这里假设$|A|>|B|$,则必定有$A>B$。由于$B$会被先加入$SA$中,所以我们保证了$A$和$B$之间的有序性。又因为$L$型桶是从左往右的顺序加入的,所以所有的$L$型后缀会逐步地按顺序加入到$SA$中。最后所有的$L$型前缀将会有序。对于$S$型后缀,除了要注意是相反的顺序和重新对$$后缀排序外,其余的原理与$L$型排序类似。
之前的讨论都是基于我们已知$SA_1$的情况下进行的,现在我们来考虑如何计算$SA_1$。由于$S1$也是一个字符串,计算其后缀数组时可以考虑两种情况。
- 如果$S1$中的每一个字符都不一样,则可以直接利用桶排序直接计算$SA_1$。
- 否则,递归计算$SA_1$。
2.4对LMS子串排序
到这里,SA-IS算法几乎已经结束了,只是还有一个问题需要解决,就是对LMS子串的排序。
之前我们所提及的,我们可以利用基数排序。虽然可以在$O(|S|)$的时间内完成,但是事实上,这个基数排序不但常数大而且十分复杂。
仍然使用诱导排序来完成这一任务
与之前从$SA_1$诱导到$SA$的算法一样,只是我们这里将第二步改为:
确定每个桶 $S$型桶的起始位置。将每一个 LMS 后缀的首字母(即 LMS 字符)按照任意顺序放入对应的桶中。
待算法完成,我们会获得一个$SA$数组其中$LMS$子串之间时排好了序的。
为什么这个算法是正确的,我们需要扯到一个新的概念:LMS前缀(这个概念看上去应该是个后缀…但是原论文就是把它叫做前缀,这里也就尊重原论文的说法)
规定LMS前缀函数$pre(S,i)$表示$(1)$如果$suffix(S,i)$是$*$型的,则$pre(S,i)=S_i$即LMS字符的LMS前缀就是自己,所以上面说到的步骤就是将所有长度为$1$的LMS前缀按任意顺序放入对应的桶中。$(2)$否则是从$s_i$开始,到右边第一个LMS字符之间(包括首尾)的子串。同样的按照$suffix(S,i)$的后缀类型的不同,LMS前缀$pre(S,i)$也同样分为$S$型和$L$型。例如,在$mmiissiissiippii$中,$pre(S,3)=S_3=i$而$pre(S,4)=S[4,7]=issi$。
LMS前缀之间的字典序比较遵循LMS子串中的规定(即考虑后缀类型),毕竟它们是LMS子串的子串。

运行示例
下面将用$aabaaaab$作为输入字符串,展示计算其后缀数组的每一步。希望能通过这个示例能够更清晰地展现 SA-IS 算法的运作流程。由于涉及到对桶的操作,这里用 @ 表示正在被处理的元素,而用 ^ 表示每个桶的起始位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
0 1 2 3 4 5 6 7 8
S: a a b a a a a b #
扫描后缀类型
t: S S L S S S S L S
LMS characters: * *
|# | a | b | # 桶的名称
SA: -1|-1 -1 -1 -1 -1 -1|-1 -1
对LMS子串进行排序
1. 放入LMS子串
SA: 08|-1 -1 -1 -1 -1 03|-1 -1
2. 从*型LMS前缀诱导到L型LMS前缀
SA: 08|-1 -1 -1 -1 -1 03|-1 -1
@^ ^ ^
SA: 08|-1 -1 -1 -1 -1 03|07 -1
^ ^ @ ^
SA: 08|-1 -1 -1 -1 -1 03|07 02 # pre(S, 6)不是L型的
^ ^ @ ^
SA: 08|-1 -1 -1 -1 -1 03|07 02
^ ^ @^
SA: 08|-1 -1 -1 -1 -1 03|07 02
3. 从L型LMS前缀诱导到S型前缀
SA: 08|-1 -1 -1 -1 -1 03|07 02
^ ^ @^
SA: 08|-1 -1 -1 -1 -1 01|07 02
^ ^ @ ^
SA: 08|-1 -1 -1 -1 06 01|07 02
^ ^ @ ^
SA: 08|-1 -1 -1 00 06 01|07 02
^ ^ @ ^
SA: 08|-1 -1 05 00 06 01|07 02 # 不存在pre(S, -1)
^ ^ @ ^
SA: 08|-1 -1 05 00 06 01|07 02
^ ^ @ ^
SA: 08|-1 04 05 00 06 01|07 02
^ ^ @ ^
SA: 08|03 04 05 00 06 01|07 02
^ @^ ^
SA: 08|03 04 05 00 06 01|07 02 # pre(S, 7)不是S型的
@^ ^ ^
SA: 08|03 04 05 00 06 01|07 02
扫描并重命名LMS子串
name: 1 2
S1: 2 1 0
由于每一个字符都不一样,直接计算SA1
SA1: 2 1 0
从SA1诱导到SA
|$ | a | b |
SA: -1|-1 -1 -1 -1 -1 -1|-1 -1
1. 按照SA1的原顺序放入(忽略S1最后的字符)
SA: 08|-1 -1 -1 -1 -1 03|-1 -1
^ ^ ^
2. 从*型后缀诱导到L型后缀
SA: 08|-1 -1 -1 -1 -1 03|-1 -1
@^ ^ ^
SA: 08|-1 -1 -1 -1 -1 03|07 -1
^ ^ @ ^
SA: 08|-1 -1 -1 -1 -1 03|07 02
^ ^ @ ^
SA: 08|-1 -1 -1 -1 -1 03|07 02
^ ^ @^
3. 从L型后缀诱导到S型后缀
SA: 08|-1 -1 -1 -1 -1 03|07 02
^ ^ @^
SA: 08|-1 -1 -1 -1 -1 01|07 02
^ ^ @ ^
SA: 08|-1 -1 -1 -1 06 01|07 02
^ ^ @ ^
SA: 08|-1 -1 -1 00 06 01|07 02
^ ^ @ ^
SA: 08|-1 -1 05 00 06 01|07 02
^ ^ @ ^
SA: 08|-1 -1 05 00 06 01|07 02
^ ^ @ ^
SA: 08|-1 04 05 00 06 01|07 02
^ ^ @ ^
SA: 08|03 04 05 00 06 01|07 02 # pre(S, 2)是L型
^ @^ ^
SA: 08|03 04 05 00 06 01|07 02
@^ ^ ^
后缀数组构造完毕
SA: 8 3 4 5 0 6 1 7 2
return SA
|
具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
|
// 后缀类型
#define L_TYPE 0
#define S_TYPE 1
// 判断一个字符是否为LMS字符
inline bool is_lms_char(int *type, int x) {
return x > 0 && type[x] == S_TYPE && type[x - 1] == L_TYPE;
}
// 判断两个LMS子串是否相同
inline bool equal_substring(int *S, int x, int y, int *type) {
do {
if (S[x] != S[y])
return false;
x++, y++;
} while (!is_lms_char(type, x) && !is_lms_char(type, y));
return S[x] == S[y];
}
// 诱导排序(从*型诱导到L型、从L型诱导到S型)
// 调用之前应将*型按要求放入SA中
inline void induced_sort(int *S, int *SA, int *type, int *bucket, int *lbucket,
int *sbucket, int n, int SIGMA) {
for (int i = 0; i <= n; i++)
if (SA[i] > 0 && type[SA[i] - 1] == L_TYPE)
SA[lbucket[S[SA[i] - 1]]++] = SA[i] - 1;
for (int i = 1; i <= SIGMA; i++) // Reset S-type bucket
sbucket[i] = bucket[i] - 1;
for (int i = n; i >= 0; i--)
if (SA[i] > 0 && type[SA[i] - 1] == S_TYPE)
SA[sbucket[S[SA[i] - 1]]--] = SA[i] - 1;
}
// SA-IS主体
// S是输入字符串,length是字符串的长度, SIGMA是字符集的大小
static int *SAIS(int *S, int length, int SIGMA) {
int n = length - 1;
int *type = new int[n + 1]; // 后缀类型
int *position = new int[n + 1]; // 记录LMS子串的起始位置
int *name = new int[n + 1]; // 记录每个LMS子串的新名称
int *SA = new int[n + 1]; // SA数组
int *bucket = new int[SIGMA]; // 每个字符的桶
int *lbucket = new int[SIGMA]; // 每个字符的L型桶的起始位置
int *sbucket = new int[SIGMA]; // 每个字符的S型桶的起始位置
// 初始化每个桶
memset(bucket, 0, sizeof(int) * (SIGMA + 1));
for (int i = 0; i <= n; i++)
bucket[S[i]]++;
for (int i = 1; i <= SIGMA; i++) {
bucket[i] += bucket[i - 1];
lbucket[i] = bucket[i - 1];
sbucket[i] = bucket[i] - 1;
}
// 确定后缀类型(利用引理2.1)
type[n] = S_TYPE;
for (int i = n - 1; i >= 0; i--) {
if (S[i] < S[i + 1])
type[i] = S_TYPE;
else if (S[i] > S[i + 1])
type[i] = L_TYPE;
else
type[i] = type[i + 1];
}
// 寻找每个LMS子串
int cnt = 0;
for (int i = 1; i <= n; i++)
if (type[i] == S_TYPE && type[i - 1] == L_TYPE)
position[cnt++] = i;
// 对LMS子串进行排序
fill(SA, SA + n + 1, -1);
for (int i = 0; i < cnt; i++)
SA[sbucket[S[position[i]]]--] = position[i];
induced_sort(S, SA, type, bucket, lbucket, sbucket, n, SIGMA);
// 为每个LMS子串命名
fill(name, name + n + 1, -1);
int lastx = -1, namecnt = 1; // 上一次处理的LMS子串与名称的计数
bool flag = false; // 这里顺便记录是否有重复的字符
for (int i = 1; i <= n; i++) {
int x = SA[i];
if (is_lms_char(type, x)) {
if (lastx >= 0 && !equal_substring(S, x, lastx, type))
namecnt++;
// 因为只有相同的LMS子串才会有同样的名称
if (lastx >= 0 && namecnt == name[lastx])
flag = true;
name[x] = namecnt;
lastx = x;
}
} // for
name[n] = 0;
// 生成S1
int *S1 = new int[cnt];
int pos = 0;
for (int i = 0; i <= n; i++)
if (name[i] >= 0)
S1[pos++] = name[i];
int *SA1;
if (!flag) {
// 直接计算SA1
SA1 = new int[cnt + 1];
for (int i = 0; i < cnt; i++)
SA1[S1[i]] = i;
} else
SA1 = SAIS(S1, cnt, namecnt); // 递归计算SA1
// 从SA1诱导到SA
lbucket[0] = sbucket[0] = 0;
for (int i = 1; i <= SIGMA; i++) {
lbucket[i] = bucket[i - 1];
sbucket[i] = bucket[i] - 1;
}
fill(SA, SA + n + 1, -1);
for (int i = cnt - 1; i >= 0; i--) // 这里是逆序扫描SA1,因为SA中S型桶是倒序的
SA[sbucket[S[position[SA1[i]]]]--] = position[SA1[i]];
induced_sort(S, SA, type, bucket, lbucket, sbucket, n, SIGMA);
// 后缀数组计算完毕
return SA;
}
|
XJ的孔姥爷较通俗易懂版:
比如:
1
2
3
|
a a b a a b b a c b a b #
S S L S S L L S L L S L S
* * * *
|
那么LMS子串就是$[4,8],[8,11],[11,13]$
然后我们将这些子串排序得到$\left{2,4,3,1\right}$。(大概就是$rk$)
可以证明的是,如果两个后缀的位置同属于lms子串的分界点,那么这两个后缀的比较相当于在排序后的LMS子串的后缀比较。
比如$[8,13],[11,13]$的比较就可以转换成$431,31$的比较。
如果子串互不相等,相当于倍增后缀排序里字符两两不同一样,直接桶排序即可。
那么如果排序中存在LMS子串相等的情况呢?递归处理lms子串的SA-IS结果即可。
然后我们只需要处理通过lms子串倒推所有串的关系。我们假设这部分和之前排序lms子串的部分复杂度都是$F(n)$
那么就有$T(n)=T(n/2)+F(n)$
代码:
原:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
void SA_IS(int n,int m,int *s,int *op,int *pos)
{
int tot=0,cnt=0;int *S=s+n;//为了减少常数,这里直接取一段没有用过的地址而不是重新申请。
op[n]=0;//为了方便,钦定最后一位是S型
for(re int i=n-1;i;i--) op[i]=(s[i]!=s[i+1])?s[i]>s[i+1]:op[i+1];//O(n)求op
rk[1]=0;
for(re int i=2;i<=n;i++)
if(op[i-1]==1 && op[i]==0) pos[++tot]=i,rk[i]=tot;//求出所有lms子串的端点
else rk[i]=0;
sa_sort(pos,n,m,s,op,tot);//排序lms子串。具体实现在后面
int u=0,p=0;
for(re int i=1;i<=n;i++)//去重,即unique
if(rk[sa[i]])
{
u=rk[sa[i]];
if(cnt<=1 || pos[u+1]-pos[u]!=pos[p+1]-pos[p]) ++cnt;//一个减小常数的优化:如果两个lms子串长度不一样,一定不同
else
{
for(re int j=0;j<=pos[u+1]-pos[u];j++)//暴力判断。注意这里如果某个字符对应的lms后缀不同,也应当认为不同,因为如果首字母相同,L型后缀字典序一定大于S型。
if(s[pos[u]+j]!=s[pos[p]+j] || op[pos[u]+j]!=op[pos[p]+j]){++cnt;break;}//因为lms子串总长度不超过 $O(n)$,所以暴力扫描复杂度是对的。
}
S[u]=cnt;//重新标号。
p=u;
}
if(tot!=cnt) SA_IS(tot,cnt,S,op+n,pos+n);//cnt相当于不同数字个数,如果cnt==tot相当于所有数字两两相同,直接桶排序。为了方便,op和pos也直接取一段没有用过的地址。
else for(re int i=1;i<=tot;i++) sa[S[i]]=i;
for(re int i=1;i<=tot;i++) S[i]=pos[sa[i]];//得到真正的排名(之前的标号排的是lms子串,这里的排名是lms后缀)。
sa_sort(S,n,m,s,op,tot);//利用lms子串得到真正的sa。
}
|
菜鸡的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void SA_IS(int n,int m,int *s,int *tp,int *pos)
{
int tot=0,cnt=0;int *S=s+n;//为了减小常数,这里直接取一段没有用过的地址而不是重新申请。
tp[n]=0;//为了方便,钦定最后一位是S型
L(i,1,n-1) tp[i]=(s[i]!=s[i+1])?s[i]>s[i+1]:tp[i+1];
rk[1]=0;
R(i,2,n) if(tp[i-1]==1&&!tp[i]) pos[++tot]=i,rk[i]=tot;else rk[i]=0;//求出所有LMS子串的端点
SA_sort(pos,n,m,s,tp,tot);//排序LMS子串
int u=0,p=0;
R(i,1,n) if(rk[sa[i]]) //去重,即unique
{
u=rk[sa[i]];
if(cnt<=1||pos[u+1]-pos[u]!=pos[p+1]-pos[p]) ++cnt;//一个减小常数的优化:如果两个LMS子串长度不一样,显然这两个子串不同
else
{
R(j,0,pos[u+1]-pos[u]) //暴力判断,注意这里如果某个字符对应的LMS后缀不同,也应当认为不同,因为如果首字母相同,L型后缀字典序一定大于S型
if(s[pos[u]+j]!=s[pos[p]+j]||tp[pos[u]+j]!=tp[pos[p]+j]) {++cnt;break;}//因为LMS子串长度不超过$O(N)$,所以暴力扫描复杂度是对的。
}
S[u]=cnt;//重新标号
p=u;
}
if(tot!=cnt) SA_IS(tot,cnt,S,tp+n,pos+n);//cnt相当于不相同数字个数,如果cnt==tot相当于所有数字两两不同,直接桶排序。为了方便,tp和pos也直接取一段没有用过的地址。
else R(i,1,tot) sa[S[i]]=i;
R(i,1,tot) S[i]=pos[sa[i]];//得到真正的排名(之前的标号排的是LMS子串,这里的排名是LMS后缀)。
SA_sort(S,n,m,s,tp,tot);////利用LMS子串得到真正的sa。
}
|
为了方便考虑第二次,即通过LMS子串的后缀数组倒推所有串的后缀数组。
我们把每个LMS子串左侧部分看做是一条链,也就是说现在有若干个已知递增的序列,要归并成一个完整序列,且数字大小不超过字典序。这本质上就是多路归并。
举个例子比如字符串$\text{aabcabbacacacaa}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
a a b c a b b a c a c a c a a #
S S S L S L L S L S L S L L L S
* * * * *
# *|
a# |
aa# |
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# |
acaa# *|
acacaa# *|
acacacaa# *|
bacacacaa# |
bbacacacaa# |
bcabbacacacaa# |
caa# |
cabbacacacaa# |
cacaa# |
cacacaa# |
|
首先先随便钦定一个位置。这个位置必须满足符合首字母的区间以及LMS子串的相对位置。
比如$\texttt {abbacacacaa#}$子串可以放在$2,3,4,5,6$位置但是不能放在$1$,因为$1$的首字母不是$a$
而$\texttt{acaa#}$可以放在$3,4,5,6,7$位置,但是一定要放在$\texttt{abbacacacaa#}$之后
这里采用一种比较方便的钦定方式:倒序放入区间末尾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# *| #
a# |
aa# |
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa#
acaa# *| acaa#
acacaa# *| acacaa#
acacacaa# *| acacacaa#
bacacacaa# |
bbacacacaa# |
bcabbacacacaa# |
caa# |
cabbacacacaa# |
cacaa# |
cacacaa# |
|
然后我们先处理出所有$\texttt L$型后缀,我们考虑用已知的$SA$去推未知的。
具体来说,当前$SA$位置上有少数已经排好序的点,其余全是$0$
我们从左往右按顺序找到一个已经排好序且存在前缀的点$SA_i$,我们想插入的后缀是$SA_i-1$
首先这个操作前提是$SA_i-1$是一个$\texttt L$型后缀。然后可以发现,因为是"在开头加上一个字符",当前处理的这个串是以这个串首字母为开头且未被放入的串中最大的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# *| # <-# <=i
a# | a# <-a <=sa[i]-1
aa# |
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa#
acaa# *| acaa#
acacaa# *| acacaa#
acacacaa# *| acacacaa#
bacacacaa# | <-b
bbacacacaa# |
bcabbacacacaa# |
caa# | <-c
cabbacacacaa# |
cacaa# |
cacacaa# |
|
首先所以指针都移到最开头。
当前$i=1$,那么下一个就是$\texttt{a#}$。直接赋值给$a$指针对应位置,然后$a$指针下移一位。
然后对于串$\texttt{a#}$,下一项是$\texttt{aa#}$,同样移动。
然后处理完所有$\texttt{L}$型后变成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# *| #
a# | a#
aa# | aa#
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa# <-a
acaa# *| acaa#
acacaa# *| acacaa#
acacacaa# *| acacacaa#
bacacacaa# | bacacacaa#
bbacacacaa# | <-b
bcabbacacacaa# | bcabbacacacaa#
caa# | caa#
cabbacacacaa# | cabbacacacaa#
cacaa# | cacaa#
cacacaa# | cacacaa#
| <-c
|
然后我们恢复所有指针位置,对应到最末尾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# *| #
a# | a#
aa# | aa#
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa#
acaa# *| acaa#
acacaa# *| acacaa#
acacacaa# *| acacacaa# <-a <=sa[i]-1
bacacacaa# | bacacacaa#
bbacacacaa# |
bcabbacacacaa# | bcabbacacacaa# <-b
caa# | caa#
cabbacacacaa# | cabbacacacaa#
cacaa# | cacaa#
cacacaa# | cacacaa# <-c <=i
|
然后我们需要从后往前所有$\texttt S$型后缀的部分。同$\texttt L$型后缀,这样所有处理的后缀都是同字符开头且当前未添加的后缀中最大的。
我们发现一点:$\texttt{cacacaa#}$的上一个前缀是$\texttt{acacacaa#}$。其实直接赋值就可以了。
然后按顺序处理:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# *| #
a# | a#
aa# | aa#
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa# <-a <=sa[i]-1
acaa# *| acaa#
acacaa# *| acacaa#
acacacaa# *| acacacaa#
bacacacaa# | bacacacaa#
bbacacacaa# | bbacacacaa# <-b
bcabbacacacaa# | bcabbacacacaa# <=i
caa# | caa#
cabbacacacaa# | cabbacacacaa#
cacaa# | cacaa#
cacacaa# | cacacaa# <-c
|
这时可以发现当前位置出问题了,之前的后缀与当前要放的不符(左边一列就是后缀数组)。也就是说我们一开始的钦定出问题了。
这时候我们直接赋值即可。为什么?因为这个值一定会被下一个后缀所更新掉。
所以说,一开始的赋值只要相对位置没有问题,所在区间没有问题,最后都能得到结果。
最终数组就如左边一列所示。
然后对于LMS子串的排序呢?这个好像是乱序的啊。
这里给出结论:我们可以直接按上述方式排序。
一遍排序($\texttt L$型后缀)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
a a b c a b b a c a c a c a a #
S S S L S L L S L S L S L L L S
* * * * *
# *| # <-#
a# | a# <-a
aa# | aa#
aabcabbacacacaa# |
abbacacacaa# *|
abcabbacacacaa# | abbacacacaa#
acaa# *| acacacaa#
acacaa# *| acacaa#
acacacaa# *| acaa#
bacacacaa# | bacacacaa#
bbacacacaa# | bbacacacaa#
bcabbacacacaa# | <-b
caa# | caa#
cabbacacacaa# | cabbacacacaa#
cacaa# | cacacaa#
cacacaa# | cacaa#
| <-c
|
最终排序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# *| # *
a# | a#
aa# | aa#
aabcabbacacacaa# | aabcabbacacacaa#
abbacacacaa# *| abbacacacaa# *
abcabbacacacaa# | abcabbacacacaa#
acaa# *| acaa# *
acacaa# *| acacacaa# *
acacacaa# *| acacaa# *
bacacacaa# | bacacacaa#
bbacacacaa# | bbacacacaa#
bcabbacacacaa# | bcabbacacacaa#
caa# | caa#
cabbacacacaa# | cabbacacacaa#
cacaa# | cacacaa#
cacacaa# | cacaa#
|
上面右排带$\texttt *$的就是排序后所有LMS子串的对应位置。
但是$8$和$10$是不是错了啊!
注意我们排的并不是后缀,而是一个子串。而$[8,10]$和$[10,12]$是本质相同的,所以怎么排都不算错。
对于正确性,一个感性的理解就是:如果一个串$a>b$且$a$排在$b$前,那么$a$通过一系列$\texttt L$和$\texttt S$后将会把$b$排到自己前面。
然后回到上例,这里$[8,10]$和$[10,12]$本质相同,所以最后去重时发现不是两两相同的,递归处理。
那么递归处理的串就是$\texttt{24431}$。
处理结束后返回的是$\texttt{25431}$。
然后根据上面的过程诱导排序即可。
总复杂度$O(n)$。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1000010
#define re register
using namespace std;
char str[N];
int sa[N],rk[N],h[N],s[N<<1],op[N<<1],pos[N<<1],c1[N],c[N];
#define L(x) sa[c[s[x]]--]=x
#define R(x) sa[c[s[x]]++]=x
inline void sa_sort(int *S,int n,int m,int *s,int *op,int tn)
{
for(re int i=1;i<=n;i++) sa[i]=0;
for(re int i=1;i<=m;i++) c1[i]=0;
for(re int i=1;i<=n;i++) c1[s[i]]++;
for(re int i=2;i<=m;i++) c1[i]+=c1[i-1];
for(re int i=1;i<=m;i++) c[i]=c1[i];
for(re int i=tn;i;i--) L(S[i]);
for(re int i=1;i<=m+1;i++) c[i]=c1[i-1]+1;
for(re int i=1;i<=n;i++)
if(sa[i]>1 && op[sa[i]-1]) R(sa[i]-1);
for(re int i=1;i<=m;i++) c[i]=c1[i];
for(re int i=n;i;i--)
if(sa[i]>1 && !op[sa[i]-1]) L(sa[i]-1);
}
void SA_IS(int n,int m,int *s,int *op,int *pos)
{
int tot=0,cnt=0;int *S=s+n;
op[n]=0;
for(re int i=n-1;i;i--) op[i]=(s[i]!=s[i+1])?s[i]>s[i+1]:op[i+1];
rk[1]=0;
for(re int i=2;i<=n;i++)
if(op[i-1]==1 && op[i]==0) pos[++tot]=i,rk[i]=tot;
else rk[i]=0;
sa_sort(pos,n,m,s,op,tot);
int u=0,p=0;
for(re int i=1;i<=n;i++)
if(rk[sa[i]])
{
u=rk[sa[i]];
if(cnt<=1 || pos[u+1]-pos[u]!=pos[p+1]-pos[p]) ++cnt;
else
{
for(re int j=0;j<=pos[u+1]-pos[u];j++)
if(s[pos[u]+j]!=s[pos[p]+j] || op[pos[u]+j]!=op[pos[p]+j]){++cnt;break;}
}
S[u]=cnt;
p=u;
}
if(tot!=cnt) SA_IS(tot,cnt,S,op+n,pos+n);
else for(re int i=1;i<=tot;i++) sa[S[i]]=i;
for(re int i=1;i<=tot;i++) S[i]=pos[sa[i]];
sa_sort(S,n,m,s,op,tot);
}
int ht[N];
void get_ht(int n)
{
for(re int i=1;i<=n;i++) rk[sa[i]=sa[i+1]]=i;
for(re int i=1,p=0;i<=n;ht[rk[i]]=p,i++)
if(rk[i]!=1) for(p=p-!!p;sa[rk[i]-1]+p<=n && i+p<=n && s[i+p]==s[sa[rk[i]-1]+p];p++);
}
namespace IO
{
char obuf[(1<<21)+1],st[11],*oS=obuf,*oT=obuf+(1<<21);
void Flush(){fwrite(obuf,1,oS-obuf,stdout),oS=obuf;}
void Put(char x){*oS++=x;if(oS==oT)Flush();}
void write(int x){int top=0;if(!x)Put('0');while(x)st[++top]=(x%10)+48,x/=10;while(top)Put(st[top--]);Put(' ');}
}using namespace IO;
int main()
{
int n;
fread(str+1,1,100000,stdin),n=strlen(str+1);
while(!isalpha(str[n])) --n;
for(int i=1;i<=n;i++) s[i]=str[i]-'a'+2;
s[++n]=1;
SA_IS(n--,28,s,op,pos);
get_ht(n);
for(int i=1;i<=n;i++) write(sa[i]);Put('\n');
for(int i=2;i<=n;i++) write(ht[i]);Flush();
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
|
#include<bits/stdc++.h>
#define ld long double
#define tset puts("qwq");
#define test puts("QAQ");
#define pb(a) push_back(a)
#define pii pair<int,int>
#define mkp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
//#define int long long
#define R(i,a,b) for(int i=(a),i##E=(b);i<=i##E;i++)
#define L(i,a,b) for(int i=(b),i##E=(a);i>=i##E;i--)
#define clr(f,n) memset(f,0,sizeof(int)*(n))
#define cpy(f,g,n) memcpy(f,g,sizeof(int)*(n))
#define Swap(x,y) (x^=y^=x^=y)
template <typename T> bool ckmax(T &x, T y) { return x<y?x=y,true:false;}
template <typename T> bool ckmin(T &x, T y) { return x>y?x=y,true:false;}
using namespace std;
//const ll inf=0x7f7f7f7f7f7f7f3f;
const ll inf=(1ll<<60);
//const int inf=0x7f7f7f7f;
//const int mod=1e9+7;
const double Pi=acos(-1);
const int mod=998244353;
const double eps=1e-6;
inline int fpow(int a,int b=mod-2,int p=mod){int res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;}
/*
const int qwq=2000010;
int F[qwq],inv[qwq],Finv[qwq];
void init_C()
{
F[0]=Finv[0]=inv[1]=1;
R(i,2,qwq-10) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
R(i,1,qwq-10) F[i]=1ll*(F[i-1]*i)%mod,Finv[i]=1ll*(Finv[i-1]*inv[i])%mod;
}
inline int C(int n,int m){ if(m<0||m>n||n<0) return 0;return 1ll*F[n]%mod*1ll*Finv[m]*1ll%mod*1ll*Finv[n-m]%mod;}
*/
//#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
inline ll read()
{
char c=getchar();ll x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;
return x;
}
inline void write(ll x){if (x<0){putchar('-');write(-x);return;}if (x>=10) write(x/10);putchar(x%10+'0');}
inline void writesp(ll x){write(x),putchar(' ');}
inline void writeln(ll x){write(x);putchar('\n');}
/*
unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
mt19937 rand_num(seed);
uniform_int_distribution<long long> dist(0, 10000000); // ¸ø¶¨·¶Î§
printf("%lld ",dist(rand_num));
*/
const int N=2e6+10;
char str[N];
int n;
int s[N],sa[N],rk[N],tp[N],pos[N],c[N],c1[N];
#define del(x) sa[c[s[x]]--]=x
#define add(x) sa[c[s[x]]++]=x
void SA_sort(int *S,int n,int m,int *s,int *tp,int tot)
{
clr(sa,n+2);clr(c1,m+2);
R(i,1,n) c1[s[i]]++;
R(i,2,m) c1[i]+=c1[i-1];
cpy(c+1,c1+1,m+2);
L(i,1,tot) del(S[i]);
R(i,1,m+1) c[i]=c1[i-1]+1;
R(i,1,n) if(sa[i]>1&&tp[sa[i]-1]) add(sa[i]-1);
cpy(c+1,c1+1,m+2);
L(i,1,n) if(sa[i]>1&&!tp[sa[i]-1]) del(sa[i]-1);
}
void SA_IS(int n,int m,int *s,int *tp,int *pos)
{
int tot=0,cnt=0;int *S=s+n;//为了减小常数,这里直接取一段没有用过的地址而不是重新申请。
tp[n]=0;//为了方便,钦定最后一位是S型
L(i,1,n-1) tp[i]=(s[i]!=s[i+1])?s[i]>s[i+1]:tp[i+1];
rk[1]=0;
R(i,2,n) if(tp[i-1]==1&&!tp[i]) pos[++tot]=i,rk[i]=tot;else rk[i]=0;//求出所有LMS子串的端点
SA_sort(pos,n,m,s,tp,tot);//排序LMS子串
int u=0,p=0;
R(i,1,n) if(rk[sa[i]]) //去重,即unique
{
u=rk[sa[i]];
if(cnt<=1||pos[u+1]-pos[u]!=pos[p+1]-pos[p]) ++cnt;//一个减小常数的优化:如果两个LMS子串长度不一样,显然这两个子串不同
else
{
R(j,0,pos[u+1]-pos[u]) //暴力判断,注意这里如果某个字符对应的LMS后缀不同,也应当认为不同,因为如果首字母相同,L型后缀字典序一定大于S型
if(s[pos[u]+j]!=s[pos[p]+j]||tp[pos[u]+j]!=tp[pos[p]+j]) {++cnt;break;}//因为LMS子串长度不超过$O(N)$,所以暴力扫描复杂度是对的。
}
S[u]=cnt;//重新标号
p=u;
}
if(tot!=cnt) SA_IS(tot,cnt,S,tp+n,pos+n);//cnt相当于不相同数字个数,如果cnt==tot相当于所有数字两两不同,直接桶排序。为了方便,tp和pos也直接取一段没有用过的地址。
else R(i,1,tot) sa[S[i]]=i;
R(i,1,tot) S[i]=pos[sa[i]];//得到真正的排名(之前的标号排的是LMS子串,这里的排名是LMS后缀)。
SA_sort(S,n,m,s,tp,tot);////利用LMS子串得到真正的sa。
}
int ht[N];
void get_ht(int n)
{
R(i,1,n) rk[sa[i]=sa[i+1]]=i;
int k=0;
R(i,1,n)
{
if(k) --k;
while(s[i+k]==s[sa[rk[i]-1]+k]) ++k;
ht[rk[i]]=k;
}
}
namespace IO
{
char obuf[(1<<21)+1],st[11],*oS=obuf,*oT=obuf+(1<<21);
void Flush(){fwrite(obuf,1,oS-obuf,stdout),oS=obuf;}
void Put(char x){*oS++=x;if(oS==oT)Flush();}
void write(int x){int top=0;if(!x)Put('0');while(x)st[++top]=(x%10)+48,x/=10;while(top)Put(st[top--]);Put(' ');}
}using namespace IO;
signed main()
{
fread(str+1,1,100000,stdin);n=strlen(str+1);
while(!isalpha(str[n])) --n;
R(i,1,n) s[i]=str[i]-'a'+2;
s[++n]=1;
//writeln(n);R(i,1,n) writesp(s[i]);puts("");
SA_IS(n--,28,s,tp,pos);
get_ht(n);
R(i,1,n) write(sa[i]);Put('\n');
R(i,2,n) write(ht[i]);Flush();
return 0;
}
|
附一道需要用的题(卡$\texttt{SAM}$)
DC3 :
不会
获取$height$数组
LCP(最长公共前缀)
$S(i)$表示从位置$i$开始的后缀
两个字符串$S$和$T$的$LCP$就是最大的$x(x\leq\min(|S|,|T|))$使得$S_i=T_i(\forall1\leq i\leq x)$。
这里使用$LCP(i,j)$表示$S(i)$和$S(j)$的最长公共前缀
$lcp(i,j)$表示$lcp(i,j)$表示后缀$i$和后缀$j$的最长公共前缀(的长度)。
height数组的定义
$height[i]=lcp(sa[i],sa[i-1])$,即第$i$名的后缀与它前一名的前缀的最长公共前缀。
$height[1]$可以视为$0$。
这里使用$h[i]$表示$height[rk[i]]$
接下来是一些性质以及证明
$1. lcp(sa[i],sa[j])=\min(lcp(sa[i],sa[k]),lcp(sa[k],sa[j]))$
放个盗来的图(以$aaaaabaaab$为例,下面的数组是$sa$)
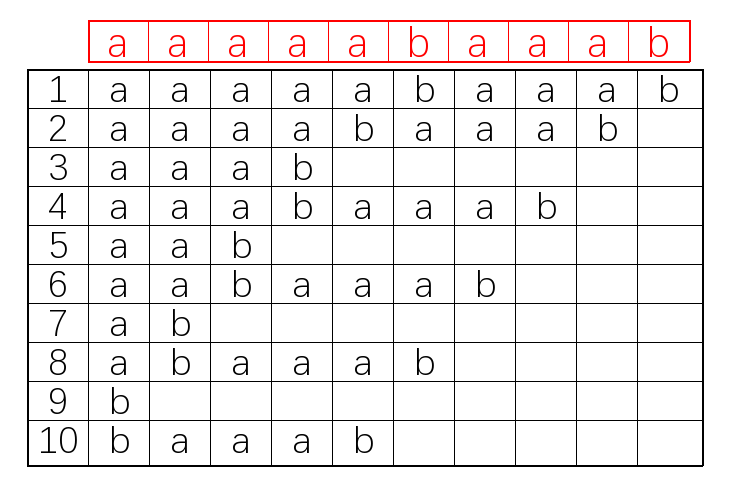
证明:
设$I=S(sa[i]),J=S(sa[j]),K=S(sa[k]),p=\min(lcp(sa[i],sa[k]),lcp(sa[k],sa[j]))$。
则$I$与$K$的前$p$个字符相同,$K$与$J$的前$p$个字符相同。所以$I$和$J$至少有前$p$个字符相同
由$p=\min(lcp(sa[i],sa[k]),lcp(sa[k],sa[j]))$,可知$I$与$K$第$p+1$个字符不相同,或者$J$与$K$的第$p+1$个字符不相同。
所以$I$和$J$最长公共前缀为$p$。
$2. h[i]\ge h[i-1]-1$(重点)
对于$h[i-1]\leq 1$时显然成立。
考虑$h[i-1]>1$的情况:
设$k$为$sa[rk[i-1]-1]$。
则$h[i-1]=LCP(i-1,k)$
把$S(i-1)$和$S(k)$去掉首字母,得到$S(i)$和$S(k+1)$,可知
$LCP(i,k+1)=LCP(i-1,k)-1=h[i-1]-1$
同时$k+1$在$sa$一定在$i$的前面
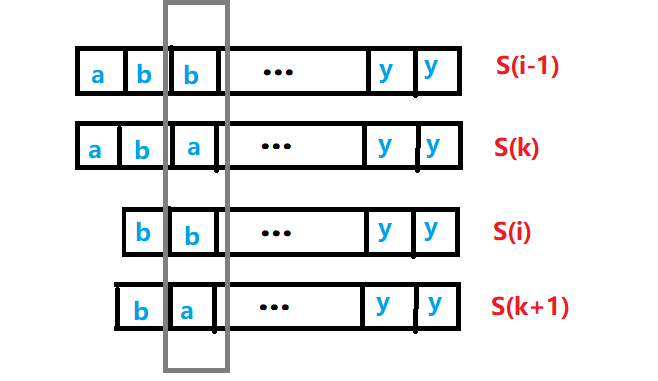
$S(k)$之所以在$S(i-1)$的前面,就是在第$LCP(i-1,k)+1$的字符差异导致的。如上图灰框圈出的部分。
当去掉首字母后,因为$h[i-1]>1$,所以$S(i)$与$S(k+1)$还是会在同样它的地方有差异,$rk[k+1]$还是小于$rk[i]$,$k+1$在$sa$中一定排在$i$前面。
那么所以比$i$排名靠前的且$LCP$最大的一定是与$i$相邻的$sa[rk[i]-1]$。
则$lcp(sa[rk[i]],sa[rk[i-1]])\ge LCP(i,k+1)$
$height[rk[i]]\ge h[i-1]-1$
$h[i]\ge h[i-1]-1$
$3. lcp(sa[i],sa[j])=\min(height[k])(\forall k, i < k\leq j)$
证明:根据性质$1$
$lcp(sa[i],sa[j])$
$=\min(lcp(sa[i],sa[i+1]),lcp(sa[i+1],sa[j]))$
$=min(lcp(sa[i],sa[i+1]),lcp(sa[i+1],sa[i+2]),lcp(sa[i+2],sa[j]))$
$=\min(lcp(sa[k],sa[k-1]))(\forall k,i<k\leq j)$
$=\min(height[k])(\forall k,i<k\leq j)$
代码:
1
2
3
4
5
6
7
|
int k=0;
R(i,1,n)
{
if(k) --k;
while(s[i+k]==s[sa[rk[i]-1]+k]) ++k;
ht[rk[i]]=k;
}
|
一些应用
任意两个后缀的$LCP$
由性质$3$可知:
$LCP(i,j)=\min(height[k])(\min(rk[i],rk[j])+1<k\leq\max(rk[i],rk[j]))$
用$ST$表$O(n\log n)$预处理,$O(1)$回答。
不同子串个数
求一个子串本质不同的子串个数。
子串就是后缀的前缀,所以可以枚举每个后缀,计算前缀总数,再减掉重复。
“前缀总数"为总子串个数为$\frac{n\times(n+1)}{2}$
如果按后缀排序的顺序枚举后缀,每次新增的子串就是除了与上一个后缀的$LCP$剩下的前缀。这些前缀一定是新增的,否则会破坏$lcp(sa[i],sa[j])=\min(height[i+1\cdots j])$的性质。只有这些前缀是新增的,因为$LCP$部分在枚举上一个前缀时计算过了。
(每个后缀的所有前缀构成了所有子串。对于某一个后缀$S(i)$的前缀,与前面重复的个数为$height[rk[i]]$。)
答案即为$\frac{n\times(n+1)}{2}-\sum_{i=1}^n height[i]$
最长公共子串
求多个字符串的最长公共子串。
把每个子串依次连接起来,每个串之间用一个特殊字符隔开。再给每个串的字染上颜色。构建后缀数组。
扫一遍$sa$数组,用尺取法获取尽可能小的区间$[l,r]$使$sa[i](\forall i,l\leq i \leq r)$,能覆盖所有颜色,所有的$\min(heigt[i])(\forall i,l<i\leq r)$的最大值即为答案。用单调队列维护达到$O(\sum len(S))$
模式串出现次数
给定一些母串和模式串,求每个模式串在多少个母串里出现过。
把所有的串拼到一起建出$SA$,找到每个模式串$p$的“匹配区间”,即最大的区间$[l,r]$使所有的$LCP(i,p)\ge |p|$。答案具有单调性可以$ST$表+二分。由于模式串之间可能有子串关系,统计时染个色,模式串不加入答案,做一个前缀和即可。
去重的话可以类似于$HH$的项链(主席树,离线+树状数组,莫队等)。
可重叠最长重复子串
$\max (height[i])$
不可重叠最长重复子串
二分答案。找到所有满足$\min(height[i])\ge mid (l\leq i\leq r)$的区间(区间尽可能大),若$\max(sa[i])-\min(sa[i])\ge mid$则答案可行。(二分目标串的长度$|S|$,将$h$数组划分成若干个$LCP\ge|S|$的段,利用$RMQ$对每个段求其中出现的数最大和最小的下标,若这两个下标的距离满足条件,则一定有长度为$|S|$的字符串不重叠地出现了两次。)
[ABC141E] Who Says a Pun?
最长回文子串
枚举一下回文中心$p$,求出翻转过来之前的前缀$p$与后缀$p$的$LCP$更新答案。把串翻转过来接在后面使用$ST$表维护
最小表示法
P4051 [JSOI2007]字符加密
题意:
给定一个串,可以任意把最后面的字符移到开头,求能得到的字典序最小的串。
题解:
把原串复制一遍接在后面(不加特殊字符),两边染个色。找到染前半段颜色的$rk$最小的后缀就是答案。
出现至少 k 次的子串的最大长度
「USACO06DEC」Milk Patterns
题解:
出现至少$k$次意味着后缀排序后有至少连续$k$个后缀的$LCP$是这个子串。
所以,求出每相邻$k-1$个$height$的最小值,再求这些最小值的最大值就是答案。
可以使用单调队列$O(n)$解决。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
signed main()
{
n=read(),k=read();
R(i,1,n) a[i]=b[i]=read();
sort(b+1,b+n+1);
int tit=unique(b+1,b+n+1)-b-1;
R(i,1,n) a[i]=lower_bound(b+1,b+tit+1,a[i])-b;
get_SA(a,sa,rk,n,ht);
R(i,1,n)
{
while((int)q.size()>0&&q.front()<=i-k+1) q.pop_front();
while((int)q.size()>0&&ht[q.back()]>=ht[i]) q.pop_back();
q.pb(i);
if(i>=k-1&&(int)q.size()>0) ckmax(ans,ht[q.front()]);
}
writeln(ans);
}
|
寻找最小的循环移动位置
「JSOI2007」字符加密
将字符串$S$复制一份变成$SS$就转化成了后缀排序问题。
在字符串中找子串
在线地在主串$T$中寻找模式串$S$。
我们可以先构造出$T$的后缀数组,然后查找子串$S$。若子串$S$在$T$中出现,它必定是$T$的一些后缀的前缀。因为我们已经将所以后缀排序了,我们可以通过在$p$数组中二分$S$来实现。比较子串和当前后缀的时间复杂度为$O(|S|)$,因此找子串的时间复杂度为$O(|S|\log |T|)$。注意,如果该子串在$T$出现多次,每次都是在$p$数组中相邻的。因此出现次数可以通过再次二分找到,输出每次出现的位置也很轻松。
从字符串首尾取字符最小化字典序
「USACO07DEC」Best Cow Line
题目大意:
给你一个字符串,每次从首或尾取一个字符组成字符串,问所有能够组成的字符串中字典序最小的一个。
题解:
暴力做法就是每次最坏$O(n)$地判断当前应该取首还是尾(即比较取首得到的字符串与取尾得到的反串的大小),只需优化这一判断过程即可。
由于需要在原串后缀与反串后缀构成的集合内比较大小,可以将反串拼接在原串后,并在中间加上一个没出现过的字符(如#,代码中可以直接使用空字符),求后缀数组,即可$O(1)$完成判断
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
signed main()
{
n=read();int l=1,r=n;
R(i,1,n) while(!isalpha(s[i]=getchar()));
R(i,1,n) ss[i]=ss[2*n+2-i]=s[i];
n=2*n+1;
get_SA(ss,sa,rk,n);
while(l<=r)
{
++tit;
printf("%c",rk[l]<rk[n+1-r]?s[l++]:s[r--]);
if(tit%80==0) puts("");
}
}
|
连续的若干个相同子串
我们可以枚举连续串的长度$|S|$,按照$|S|$对整个进行分块,对相邻两块的块首进行$LCP$与$LCS$查询,具体见[2009]后缀数组——处理字符串的有力工具。
结合并查集
某些题目求解时要求你将后缀数组划分成若干个连续 LCP 长度大于等于某一值的段,亦即将$h$数组划分成若干个连续最小值大于等于某一值的段并统计每一段的答案。如果有多次询问,我们可以将询问离线。观察到当给定值单调递减的时候,满足条件的区间个数总是越来越少,而新区间都是两个或多个原区间相连所得,且新区间中不包含在原区间内的部分的$h$值都为减少到的这个值。我们只需要维护一个并查集,每次合并相邻的两个区间,并维护统计信息即可。
经典题目:「NOI2015」品酒大会。
结合线段树
某些题目让你求满足条件的前若干个数,而这些数又在后缀排序中的一个区间内。这时我们可以用归并排序的性质来合并两个结点的信息,利用线段树维护和查询区间答案。
结合单调栈
例题:「AHOI2013」差异
由于直接算答案不是很好做,考虑先求出$\sum\limits_{1\leq i < j\leq n} len(T_i)+len(T_j)$再减去后面那堆东西。
这部分答案为$\frac{n(n-1)(n+1)}{2}$(每个后缀都出现了$n-1$次,后缀总长是$\frac{n(n+1)}{2}$)
之后考虑怎么搞$lcp(i,j)$这项,我们知道$lcp(i,j)=k$等价于$\min\left{height[i+1\cdots j] \right}=k$
所以可以将$lcp(i,j)$记作$\min\left{x|i+1\leq x \leq j,height[x]=lcp(i,j) \right}$对答案的贡献。
考虑每个位置对答案的贡献是哪些后缀的$\texttt{LCP}$,其实就是从它开始向左若干个连续的$\texttt{height}$大于它的后缀选一个,再从向右若干个连续个$\texttt{height}$不小于它的后缀中选一个。这个东西可以单调栈搞。
虽然写的时候偷懒直接搞了个悬线法。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
signed main()
{
scanf("%s",str+1);
n=strlen(str+1);ans=1ll*(n+1)*n*(n-1)/2;
R(i,1,n) s[i]=str[i]-'a'+2;
get_SA(s,sa,rk,n),get_ht(n,ht);ht[n+1]=-1;
R(i,1,n) l[i]=r[i]=i;
R(i,1,n) while(ht[l[i]-1]>ht[i]) l[i]=l[l[i]-1];
L(i,1,n) while(ht[r[i]+1]>=ht[i]) r[i]=r[r[i]+1];
R(i,1,n) ans-=2ll*ht[i]*(i-l[i]+1)*(r[i]-i+1);
//L(i,1,n) printf("%lld %lld %lld %lld\n",i,i-l[i]+1,r[i]-i+1,ht[i]);
printf("%lld\n",ans);
}
|
习题





